NCERT Solutions for Class 9 Maths Exercise 1.2 Question 3

Understanding the Question 🧐
The goal is to find the exact location of the irrational number &&\sqrt{5}&& on a number line. Since we cannot measure &&\sqrt{5}&& (which is approximately &&2.236…&&) directly with a ruler, we will use a geometric method. The key to this method is the Pythagoras Theorem, which connects the sides of a right-angled triangle.
Show how &&\sqrt{5}&& can be represented on the number line.
The Strategy: Using Pythagoras Theorem 📝
The Pythagoras Theorem states: &&(\text{Base})^2 + (\text{Height})^2 = (\text{Hypotenuse})^2&&.
We want to create a triangle where the hypotenuse has a length of &&\sqrt{5}&&. So, we need:
&&(\text{Base})^2 + (\text{Height})^2 = 5&&
Let’s find two simple whole numbers whose squares add up to &&5&&. We can see that:
- &&2^2 = 4&&
- &&1^2 = 1&&
And &&4 + 1 = 5&&. Perfect! So, we will construct a right-angled triangle with a base of &&2&& units and a height of &&1&& unit. The hypotenuse of this triangle will be &&\sqrt{2^2 + 1^2} = \sqrt{4+1} = \sqrt{5}&&.
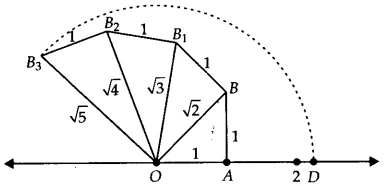
Step-by-Step Construction Guide
You will need a ruler, a compass, and a protractor for this construction.
- Draw the Number Line: Draw a straight line and mark a point &&O&& on it to represent &&0&&. Mark points at equal distances for &&1, 2, 3, \dots&& etc.
- Mark the Base: From point &&O&&, measure &&2&& units along the number line and mark this point as &&A&&. The length &&OA&& is our base.
- Draw the Height: At point &&A&&, use a protractor to draw a line perpendicular to the number line. On this perpendicular line, measure &&1&& unit and mark the point as &&B&&. The length &&AB&& is our height.
- Form the Hypotenuse: Join the points &&O&& and &&B&&. The line segment &&OB&& is the hypotenuse of the right-angled triangle &&OAB&&.
- Calculate the Hypotenuse Length: By the Pythagoras theorem, the length of &&OB&& is &&\sqrt{OA^2 + AB^2} = \sqrt{2^2 + 1^2} = \sqrt{5}&&.
- Transfer the Length: Now, place the metal tip of your compass at point &&O&& (the origin) and extend the pencil tip to point &&B&&. The distance in your compass is now exactly &&\sqrt{5}&& units.
- Locate on Number Line: Keeping the compass tip at &&O&&, draw an arc that cuts the number line. Let’s call the point where the arc intersects the positive side of the number line &&P&&.
- Final Result: The distance from &&O&& to &&P&& is the radius of the arc, which is equal to the length of &&OB&&. Therefore, the point &&P&& on the number line represents &&\sqrt{5}&&.
Conclusion and Key Points ✅
We have successfully located &&\sqrt{5}&& on the number line. The process involves two main ideas:
- Using the Pythagoras theorem to construct a physical length corresponding to an irrational number.
- Using a compass to transfer this constructed length onto the number line accurately.
- To find &&\sqrt{5}&&, we break &&5&& into &&4+1&&, which are &&2^2 + 1^2&&.
- The base of the triangle is taken on the number line itself.
- The compass acts as a tool to transfer the hypotenuse length to the linear number line.
FAQ
Q: What is the Pythagoras theorem?
A: The Pythagoras theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The formula is &&a^2 + b^2 = c^2&&.
Q: Why did we choose sides of length 2 and 1 for constructing &&\sqrt{5}&&?
A: We chose sides of length &&2&& and &&1&& because we needed two numbers whose squares add up to &&5&&. Since &&2^2 = 4&& and &&1^2 = 1&&, their sum is &&4 + 1 = 5&&. This allows us to construct a right-angled triangle with a hypotenuse of exactly &&\sqrt{5}&&.
Q: How would you represent &&\sqrt{2}&& on the number line?
A: To represent &&\sqrt{2}&&, you would construct a right-angled triangle with a base of &&1&& unit and a height of &&1&& unit, because &&1^2 + 1^2 = 2&&. The hypotenuse of this triangle would have a length of &&\sqrt{2}&&, which you can then transfer to the number line.
Q: How would you represent &&\sqrt{10}&& on the number line?
A: To represent &&\sqrt{10}&&, you can use a base of &&3&& units and a height of &&1&& unit in a right-angled triangle, because &&3^2 + 1^2 = 9 + 1 = 10&&. The hypotenuse of this triangle will have a length of &&\sqrt{10}&&.
Q: What tools do I need for this geometric construction?
A: You will need a pencil, a ruler (or scale) to measure lengths, a compass to draw arcs, and a protractor to draw the 90-degree angle accurately.
Further Reading
For a deeper understanding of number systems and geometric representations, you can refer to the official NCERT textbooks.

