NCERT Solutions for Class 9 Maths Exercise 5.1 Question 6 – Step-by-Step

Hello students! This ncert solution tackles a classic problem from **Euclidean geometry**. We will walk through a logical **geometric proof** to demonstrate the equality of two line segments based on given information and one of **Euclid’s axioms**. Understanding this process is key to building a strong foundation in geometry.
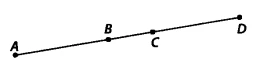
In the given figure, if &&AC = BD&&, then prove that &&AB = CD&&.
Quick Summary of the Proof 📝
| Aspect | Details |
|---|---|
| Given | Points &&A, B, C, D&& are on a line such that &&AC = BD&&. |
| To Prove | &&AB = CD&& |
| Key Axiom Used | If equals are subtracted from equals, the remainders are equal. |
How to Prove AB = CD when AC = BD 🧐
Follow these precise steps to construct the proof. A detailed explanation for each step is provided further below.
- Start with the Given Information: Begin with the equation that is given in the problem: &&AC = BD&&.
- Decompose the Line Segments: Look at the figure and express &&AC&& and &&BD&& in terms of smaller segments. &&AC&& can be written as &&AB + BC&&, and &&BD&& can be written as &&BC + CD&&.
- Substitute the Decomposed Parts: Substitute these expressions back into the original given equation. This gives you &&AB + BC = BC + CD&&.
- Apply Euclid’s Subtraction Axiom: Use Euclid’s axiom which states that ‘if equals are subtracted from equals, the remainders are equal’. Subtract the common segment &&BC&& from both sides of the equation.
- State the Final Result: After subtracting &&BC&& from both sides, you are left with &&AB = CD&&, which is what you needed to prove.
Step-by-Step Solution ✍️
Let’s perform the proof using the principles of Euclidean geometry.
Given: We are given four points &&A, B, C,&& and &&D&& on a line such that the length of segment &&AC&& is equal to the length of segment &&BD&&.
&&AC = BD&&
To Prove: We need to prove that the length of segment &&AB&& is equal to the length of segment &&CD&&.
Proof:
Step 1: Decompose the segment &&AC&&.
From the figure, we can see that the point &&B&& lies between &&A&& and &&C&&. Therefore, the total length of &&AC&& can be written as the sum of the lengths of &&AB&& and &&BC&&.
&&AC = AB + BC&& … (Equation 1)
Step 2: Decompose the segment &&BD&&.
Similarly, the point &&C&& lies between &&B&& and &&D&&. So, the total length of &&BD&& can be written as the sum of the lengths of &&BC&& and &&CD&&.
&&BD = BC + CD&& … (Equation 2)
Step 3: Substitute and use the given information.
We are given that &&AC = BD&&. We can substitute our expressions from Equation 1 and Equation 2 into this given fact.
&&AB + BC = BC + CD&&
Step 4: Apply Euclid’s Axiom.
Now, we apply Euclid’s second axiom, which states, “If equals are subtracted from equals, the remainders are equal.”
We can see that the length &&BC&& is common to both sides of our equation. Let’s subtract &&BC&& from both sides.
&& (AB + BC) – BC = (BC + CD) – BC &&
Step 5: Simplify to get the final result.
After subtracting &&BC&&, we are left with:
&&AB = CD&&
Hence, Proved.
Common Mistakes to Avoid ❌
- Visual Assumption: Don’t just assume &&AB = CD&& because it looks that way in the diagram. Geometry requires a logical proof based on given facts and axioms.
- Incorrect Decomposition: Make sure you break down the segments correctly based on the points. A common error is writing &&AC = AB + CD&&, which is incorrect.
- Forgetting the Axiom: For a complete answer, always state the axiom you are using (e.g., “If equals are subtracted from equals…”).
Real-World Application 🌍
This simple geometric principle has practical uses in manufacturing and quality control. Imagine a long metal rod from which two large, identical pieces (&&AC&& and &&BD&&) are cut. If an identical section (&&BC&&) is then removed from the same relative position on both pieces, this axiom guarantees that the remaining parts (&&AB&& and &&CD&&) will also be identical. This ensures consistency and precision in creating standardized parts.
Frequently Asked Questions (FAQ) ❓
Q: Which of Euclid’s axioms is used to solve this problem?
A: The key axiom used is Euclid’s second axiom, which states: ‘If equals are subtracted from equals, the remainders are equal.’ We use this to subtract the common segment &&BC&& from both sides of the equation.
Q: What does it mean to decompose a line segment?
A: Decomposing a line segment means expressing its length as the sum of its smaller, constituent parts. For example, if point &&B&& lies between &&A&& and &&C&&, the segment &&AC&& can be decomposed into &&AB + BC&&.
Q: Why is it important to start with the ‘Given’ information in a proof?
A: Starting with the ‘Given’ information is the foundation of any logical proof. It establishes the facts that are known to be true, from which you can build a series of logical steps to reach the desired conclusion.
Q: What is the difference between an axiom and a theorem?
A: An axiom (or postulate) is a statement that is accepted as true without proof; it’s a fundamental assumption. A theorem is a statement that has been proven to be true based on axioms and other previously proven theorems.
Further Reading 📖
To revise the fundamental axioms of Euclidean geometry, refer to your Class 9 Maths NCERT textbook. A strong grasp of these basic principles is essential for solving more complex problems. You can download the official textbook from the NCERT website: https://ncert.nic.in/.


