NCERT Solutions for Class 9 Maths Exercise 6.1 Question 4

Hello, students! In this guide, we’ll tackle Question 4 from Exercise 6.1. This is an interesting proof problem where we use the concept of angles around a point to prove that a given figure contains a straight line. Let’s get started!
| Given Information | Four angles &&x, y, w, z&& around a point O, with the condition that &&x + y = w + z&&. |
|---|---|
| To Prove | AOB is a straight line. |
| Key Concept Used | The sum of angles around a point is &&360^\circ&&, and the converse of the Linear Pair Axiom. |
Question 4: In the figure, if &&x + y = w + z&&, then prove that AOB is a line.
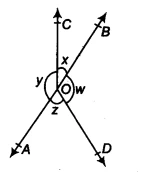
How to Prove that AOB is a Line 🤔
This proof can be completed in four simple, logical steps. This method is also outlined in the `HowTo` schema to help search engines understand our solution.
- Step 1: Use the ‘Complete Angle’ Axiom
State the fundamental axiom that the sum of all angles around a single point is &&360^\circ&&. For the given figure, this means &&x + y + z + w = 360^\circ&&. - Step 2: Substitute Using the Given Information
The problem gives the condition that &&x + y = w + z&&. Use this to substitute &&(w + z)&& in the complete angle equation with &&(x + y)&&. The equation becomes &&(x + y) + (x + y) = 360^\circ&&. - Step 3: Simplify the Equation
Combine the like terms in the new equation to get &&2(x + y) = 360^\circ&&. Solve for the sum &&(x + y)&& by dividing both sides by 2, which results in &&x + y = 180^\circ&&. - Step 4: Apply the Converse of the Linear Pair Axiom
The result &&x + y = 180^\circ&& shows that the sum of the two adjacent angles, &&x&& and &&y&&, is &&180^\circ&&. According to the converse of the linear pair axiom, if the sum of two adjacent angles is &&180^\circ&&, their non-common arms (OA and OB) must form a straight line. Therefore, AOB is a line.
Detailed Step-by-Step Proof 📝
Here is the logical flow to prove that AOB is a line.
Step 1: Sum of angles around a point
We know that the sum of all angles around a point is &&360^\circ&&. From the figure, the angles around point O are &&x, y, w,&& and &&z&&.
Therefore, we can write the equation:
&&x + y + w + z = 360^\circ&& … (Equation 1)
Step 2: Use the given condition
It is given in the problem that:
&&x + y = w + z&& … (Equation 2)
Step 3: Substitute and simplify
Now, substitute the value of &&(w + z)&& from Equation 2 into Equation 1:
&&\implies (x + y) + (x + y) = 360^\circ&&
&&\implies 2(x + y) = 360^\circ&&
&&\implies x + y = \frac{360^\circ}{2}&&
&&\implies x + y = 180^\circ&&
Step 4: Apply the Converse of the Linear Pair Axiom
We have just shown that the sum of the adjacent angles &&x&& and &&y&& is &&180^\circ&&. The axiom states that if the sum of two adjacent angles is &&180^\circ&&, then they form a linear pair, and their non-common arms form a straight line.
In this case, the non-common arms of angles &&x&& (&&\angle BOC&&) and &&y&& (&&\angle AOC&&) are OB and OA.
Since &&x + y = 180^\circ&&, OA and OB must form a straight line.
Conclusion:
Therefore, AOB is a line.
Hence, proved.
Key Concepts Used ✅
- Angles Around a Point: The sum of all angles that share a common vertex is always &&360^\circ&&.
- Converse of Linear Pair Axiom: This is the crucial final step. It’s the rule that allows you to state something is a line because its adjacent angles sum to &&180^\circ&&.
Common Mistakes to Avoid 🖍️
The most significant mistake is to assume at the start that AOB is a line and that &&x+y=180^\circ&&. You cannot do this, as “AOB is a line” is what you need to prove. The correct approach is to start with the fact that all four angles sum to &&360^\circ&&.
FAQ (Frequently Asked Questions)
Q: What is the sum of angles around a point?
A: The sum of all angles around a single point is always &&360^\circ&&. This is also known as a complete angle.
Q: What is the converse of the Linear Pair Axiom?
A: The converse of the Linear Pair Axiom states that if the sum of two adjacent angles is &&180^\circ&&, then their non-common arms form a straight line. This is the key principle used to conclude the proof in this problem.
Q: Why can’t we just assume AOB is a straight line from the beginning?
A: We cannot assume AOB is a line because that is what we need to prove. Assuming it would be circular reasoning. Instead, we must use the given information (&&x + y = w + z&&) and other axioms to logically deduce that the angles &&x&& and &&y&& add up to &&180^\circ&&, which then proves that AOB is a line.
Q: Could we also prove AOB is a line by showing w + z = 180°?
A: Yes, absolutely. Since &&x + y = w + z&& and their total sum is &&360^\circ&&, it follows that &&w + z&& must also be &&180^\circ&&. Since &&w&& and &&z&& are adjacent angles, this would also prove that AOB is a straight line.
Further Reading
For more proofs and problems related to the linear pair axiom, check out your NCERT Class 9 Maths textbook or visit the official NCERT website at https://ncert.nic.in/.


