NCERT Solutions for Class 9 Maths Exercise 7.2 Question 1

Understanding the Question 🧐
Welcome to the first question of Exercise 7.2! This problem is a great way to practice the properties of isosceles triangles. We are given an isosceles triangle &&ABC&&, where two sides are equal. Then, we have lines that cut the main angles in half (angle bisectors). Our job is to prove two relationships that arise from this setup. Let’s break down this ncert solutions problem step-by-step.
In an isosceles triangle &&ABC&&, with &&AB = AC&&, the bisectors of &&∠B&& and &&∠C&& intersect each other at &&O&&. Join &&A&& to &&O&&. Show that:
(i) &&OB = OC&&
(ii) &&AO&& bisects &&∠A&&
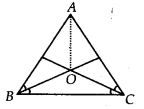
Part (i): Proving &&OB = OC&& 📝
Our goal here is to show that the lengths of the line segments &&OB&& and &&OC&& are equal. We will use the properties of the larger triangle &&ABC&& to find properties of the smaller triangle &&OBC&&.
- Start with the given information about &&ΔABC&&.
We are given that &&ΔABC&& is an isosceles triangle with &&AB = AC&&. - Use the property of isosceles triangles.
A very important theorem states that angles opposite to equal sides are equal. Therefore, in &&ΔABC&&:
&&∠ABC = ∠ACB&& - Use the information about angle bisectors.
We are told that &&OB&& bisects &&∠ABC&& and &&OC&& bisects &&∠ACB&&. This means:
&&∠OBC = \frac{1}{2}∠ABC&&
&&∠OCB = \frac{1}{2}∠ACB&& - Combine the information.
Since &&∠ABC = ∠ACB&&, their halves must also be equal. So, we can conclude that:
&&∠OBC = ∠OCB&& - Focus on &&ΔOBC&& and use the converse property.
Now look at the smaller triangle &&ΔOBC&&. We just proved it has two equal angles. The converse of the property we used earlier states that sides opposite to equal angles are equal.
In &&ΔOBC&&, the side opposite to &&∠OCB&& is &&OB&&, and the side opposite to &&∠OBC&& is &&OC&&.
Therefore:
&&OB = OC&&
And that’s the proof for the first part!
Part (ii): Proving &&AO&& bisects &&∠A&& 📝
For the second part, we need to show that the line &&AO&& divides &&∠A&& into two equal halves. The best way to do this is by proving that &&ΔOAB&& is congruent to &&ΔOAC&&.
Let’s consider &&ΔOAB&& and &&ΔOAC&&. We will use the Side-Side-Side (SSS) congruence rule.
- Side 1: &&AB = AC&&.
This is given in the problem statement. - Side 2: &&AO = AO&&.
This is the common side to both triangles. - Side 3: &&OB = OC&&.
This is what we proved in Part (i) of this question.
Since all three sides of &&ΔOAB&& are equal to the corresponding three sides of &&ΔOAC&&, by the SSS congruence rule, we have:
&&ΔOAB ≅ ΔOAC&&
Now that we know the triangles are congruent, we can say their corresponding parts are equal (by CPCTC). The angle &&∠OAB&& in the first triangle corresponds to the angle &&∠OAC&& in the second triangle.
Therefore, by CPCTC:
&&∠OAB = ∠OAC&&
Since &&AO&& divides &&∠A&& into two equal angles, we can say that &&AO&& bisects &&∠A&&. Hence Proved!
Conclusion and Key Points ✅
In this solution, we used fundamental properties of isosceles triangles. For the first part, we used the “angles opposite equal sides are equal” property to find that &&∠OBC = ∠OCB&&. Then, we used the converse property, “sides opposite equal angles are equal,” to prove &&OB = OC&&. For the second part, we used the result from the first part to satisfy the SSS congruence rule for &&ΔOAB&& and &&ΔOAC&&, which allowed us to prove &&∠OAB = ∠OAC&& by CPCTC.
- In a triangle, if two sides are equal, the angles opposite them are also equal.
- Conversely, if two angles in a triangle are equal, the sides opposite them are also equal.
- An angle bisector divides an angle into two equal parts.
- Remember the SSS congruence rule and how to use CPCTC after proving triangles are congruent.
FAQ
Q: What is the first step to prove &&OB = OC&&?
A: The first step is to use the property that in triangle &&ABC&&, angles opposite to the equal sides &&AB&& and &&AC&& are equal. This gives us &&∠ABC = ∠ACB&&. Since &&OB&& and &&OC&& are angle bisectors, we can conclude that their halves, &&∠OBC&& and &&∠OCB&&, are also equal.
Q: Which property is used to finally conclude that &&OB = OC&&?
A: After proving that &&∠OBC = ∠OCB&&, we focus on the smaller triangle, &&ΔOBC&&. In this triangle, we use the property that sides opposite to equal angles are equal. This allows us to conclude that &&OB = OC&&.
Q: How do you prove that &&AO&& bisects &&∠A&&?
A: To prove that &&AO&& bisects &&∠A&&, we prove that triangle &&OAB&& is congruent to triangle &&OAC&&. This is done using the SSS (Side-Side-Side) congruence rule. Once the triangles are proven congruent, we use CPCTC to state that &&∠OAB = ∠OAC&&.
Q: What are the three equal parts used for the SSS congruence in the second part?
A: The three pairs of equal sides are: 1. &&AB = AC&& (given in the problem). 2. &&AO = AO&& (it’s a common side to both triangles). 3. &&OB = OC&& (this was proved in the first part of the question).
Q: What is an isosceles triangle?
A: An isosceles triangle is a triangle that has at least two sides of equal length. A key property is that the angles opposite the equal sides are also equal in measure.
Q: What does it mean for a line to bisect an angle?
A: When a line or line segment bisects an angle, it divides that angle into two smaller angles that are exactly equal to each other.
Further Reading
For a deeper dive into the properties of triangles and congruence rules, make sure to read Chapter 7 of your NCERT Class 9 Maths textbook. You can find the official textbook on the NCERT website: https://ncert.nic.in/.


