NCERT Solutions for Class 9 Maths Exercise 7.2 Question 2

Understanding the Question 🧐
This question asks us to prove that a triangle is isosceles if a specific line segment, &&AD&&, is the “perpendicular bisector” of the base &&BC&&. This term holds two important clues that are key to solving the problem. Our goal is to use these clues to prove that sides &&AB&& and &&AC&& are equal. This ncert solutions guide will walk you through the proof using triangle congruence.
In &&ΔABC&&, &&AD&& is the perpendicular bisector of &&BC&&. Show that &&ΔABC&& is an isosceles triangle in which &&AB = AC&&.
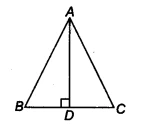
Step-by-Step Solution 📝
The solution lies in proving that the two smaller triangles, &&ΔABD&& and &&ΔACD&&, are congruent. If they are congruent, their corresponding sides &&AB&& and &&AC&& must be equal.
Step 1: Understand the Given Information
The problem states that &&AD&& is the perpendicular bisector of &&BC&&. Let’s break this down:
- Perpendicular: This means &&AD&& makes a right angle (&&90°&&) with &&BC&&. So, &&∠ADB = ∠ADC = 90°&&.
- Bisector: This means &&AD&& cuts &&BC&& into two equal halves. So, &&BD = CD&&.
Step 2: Prove that &&ΔABD ≅ ΔACD&&
Now, let’s compare the two triangles, &&ΔABD&& and &&ΔACD&&, using the information from Step 1. We will use the Side-Angle-Side (SAS) congruence rule.
- Side: &&BD = CD&&.
This is because &&AD&& is the bisector of &&BC&& (as established above). - Angle: &&∠ADB = ∠ADC&&.
Both angles are &&90°&& because &&AD&& is perpendicular to &&BC&&. This is our included angle. - Side: &&AD = AD&&.
This is the common side to both triangles.
Since we have two sides and the included angle of &&ΔABD&& equal to the corresponding parts of &&ΔACD&&, we can conclude by the SAS congruence rule:
&&ΔABD ≅ ΔACD&&
Step 3: Conclude that &&AB = AC&&
Now that we have proven the triangles are congruent, we can use the CPCTC rule (Corresponding Parts of Congruent Triangles are Congruent).
The side &&AB&& in &&ΔABD&& corresponds to the side &&AC&& in &&ΔACD&&. Therefore, by CPCTC:
&&AB = AC&&
Step 4: Final Statement
Since two sides of &&ΔABC&& (&&AB&& and &&AC&&) are equal, the triangle is an isosceles triangle.
Hence Proved.
Conclusion and Key Points ✅
This proof is a straightforward application of the SAS congruence rule. The entire solution hinges on correctly interpreting the term “perpendicular bisector” into two distinct mathematical facts: equal angles (&&90°&&) and equal segments (&&BD = CD&&). By applying these facts along with the common side &&AD&&, we easily proved that &&ΔABD ≅ ΔACD&&, which directly led to the conclusion that &&AB = AC&&, making &&ΔABC&& an isosceles triangle.
- A Perpendicular Bisector of a line segment is a line that is perpendicular to the segment and passes through its midpoint.
- SAS Congruence Rule: Two triangles are congruent if two sides and the included angle of one are equal to the corresponding two sides and included angle of the other.
- CPCTC: This stands for “Corresponding Parts of Congruent Triangles are Congruent.” It’s the reason we can state that &&AB = AC&& after proving the triangles are congruent.
FAQ
Q: What does ‘perpendicular bisector’ mean?
A: A perpendicular bisector is a line that does two things: 1. It is perpendicular (forms a &&90°&& angle) to a line segment. 2. It bisects (cuts into two equal halves) that line segment.
Q: What two conditions do we get from the statement ‘&&AD&& is the perpendicular bisector of &&BC&&’?
A: The statement gives us two key conditions: 1. &&AD&& is perpendicular to &&BC&&, which means &&∠ADB = ∠ADC = 90°&&. 2. &&AD&& bisects &&BC&&, which means &&BD = CD&&.
Q: Which congruence rule is used to solve this problem?
A: The Side-Angle-Side (SAS) congruence rule is used to prove that &&ΔABD&& is congruent to &&ΔACD&&.
Q: What are the three corresponding parts used for the SAS proof?
A: The three parts are: Side &&BD = CD&&, the included Angle &&∠ADB = ∠ADC&& (both &&90°&&), and the common Side &&AD = AD&&.
Q: How do we conclude that &&AB = AC&& after proving the triangles are congruent?
A: We use the principle of CPCTC, which stands for ‘Corresponding Parts of Congruent Triangles are Congruent’. Since &&ΔABD&& is congruent to &&ΔACD&&, their corresponding sides &&AB&& and &&AC&& must be equal.
Q: What defines an isosceles triangle?
A: A triangle is defined as isosceles if it has at least two sides of equal length. By proving &&AB = AC&&, we satisfy this condition.
Further Reading
To solidify your understanding of congruence rules, especially SAS, review the concepts in Chapter 7 of your Class 9 Maths NCERT textbook. For official resources, you can visit the NCERT website: https://ncert.nic.in/.


