NCERT Solutions for Class 9 Maths Exercise 8.2 Question 2

Welcome, students! Let’s solve Question 2 from Exercise 8.2. This is a very important proof that demonstrates a relationship between different types of quadrilaterals using the Mid-point Theorem.
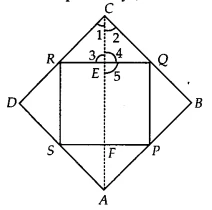
| Given Information | A rhombus ABCD, with P, Q, R, and S as the mid-points of sides AB, BC, CD, and DA, respectively. |
|---|---|
| To Prove | The quadrilateral PQRS formed by joining the mid-points is a rectangle. |
| Key Concepts Used | Mid-point Theorem, Properties of a Parallelogram, and Properties of a Rhombus’s Diagonals. |
Question 2: ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Detailed Step-by-Step Proof 📝
Given:
ABCD is a rhombus. P, Q, R, and S are the mid-points of sides AB, BC, CD, and DA.
To Prove: PQRS is a rectangle.
Construction: Join the diagonals of the rhombus, AC and BD.
Part 1: Prove that PQRS is a parallelogram
In &&\triangle ADC&&, S is the mid-point of AD and R is the mid-point of CD.
By the Mid-point Theorem, we have:
&&SR \parallel AC&& and &&SR = \frac{1}{2} AC&& … (1)
In &&\triangle ABC&&, P is the mid-point of AB and Q is the mid-point of BC.
By the Mid-point Theorem, we have:
&&PQ \parallel AC&& and &&PQ = \frac{1}{2} AC&& … (2)
From equations (1) and (2), we can conclude that:
&&PQ \parallel SR&& and &&PQ = SR&&.
Since one pair of opposite sides of quadrilateral PQRS is equal and parallel, PQRS is a parallelogram.
Part 2: Prove that one angle of the parallelogram is &&90^\circ&&
Now, let’s consider &&\triangle DAB&&. S is the mid-point of DA and P is the mid-point of AB.
By the Mid-point Theorem:
&&SP \parallel DB&& … (3)
We know a key property of a rhombus: its diagonals are perpendicular to each other.
Therefore, &&AC \perp BD&&.
Let’s consider the intersection of SR and SP. Since &&SR \parallel AC&& (from eq. 1) and &&SP \parallel DB&& (from eq. 3), the angle between SR and SP must be the same as the angle between AC and BD.
Since &&AC \perp BD&&, it means &&SR \perp SP&&.
Therefore, &&\angle RSP = 90^\circ&&.
Conclusion:
We have proved that PQRS is a parallelogram (Part 1) and that one of its interior angles is &&90^\circ&& (Part 2).
A parallelogram with one right angle is a rectangle.
Hence, the quadrilateral PQRS is a rectangle.
A Key Geometric Relationship ✅
This proof demonstrates an important relationship between quadrilaterals:
- Joining the mid-points of a rhombus gives a rectangle.
- Joining the mid-points of a rectangle gives a rhombus.
FAQ (Frequently Asked Questions)
Q: What is the Mid-point Theorem?
A: The Mid-point Theorem states that the line segment connecting the mid-points of two sides of a triangle is parallel to the third side and is half the length of the third side.
Q: What is the key property of a rhombus’s diagonals used in this proof?
A: The key property used is that the diagonals of a rhombus are perpendicular to each other (they intersect at a &&90&&-degree angle). This is essential for proving that the resulting quadrilateral PQRS has a right angle.
Q: Why is proving PQRS is a parallelogram not enough?
A: Proving that PQRS is a parallelogram is the first major step. However, the question asks us to show it is a rectangle. A rectangle is a special type of parallelogram that has all four angles equal to &&90^\circ&&. Therefore, after proving it’s a parallelogram, we must complete the second step of proving that at least one of its interior angles is a right angle.
Q: What shape is formed by joining the mid-points of a rectangle?
A: Interestingly, the converse is also true! The quadrilateral formed by joining the mid-points of the sides of a rectangle is a rhombus. The diagonals of a rectangle are equal but not perpendicular, which leads to the resulting shape having equal sides but not necessarily right angles.


