NCERT Solutions for Class 9 Maths Exercise 1.2 Question 4 (Classroom Activity)

Understanding the Activity 🧐
This question is a fun, hands-on classroom activity rather than a typical problem to solve. The goal is to construct a ‘square root spiral’, which is a beautiful geometric shape that visually represents the square roots of positive integers (like &&\sqrt{2}, \sqrt{3}, \sqrt{4}, \sqrt{5} \dots&&).
The entire construction is a creative application of the Pythagoras Theorem, which you’ll use again and again to build the spiral.
Classroom activity: Constructing the ‘square root spiral’.
Materials Needed 🛠️
- A large sheet of paper
- A sharp pencil
- A ruler (scale)
- A protractor or a set-square (to draw accurate right angles)
Step-by-Step Guide to Construction 📝
Follow these steps carefully to create your own square root spiral.
-
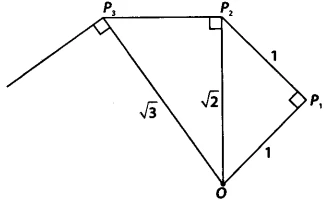
Step 1: The Foundation (Getting &&OP_1&&)
Take a point near the center of your paper and label it &&O&& (for Origin). From &&O&&, draw a straight line segment &&OP_1&& of length &&1&& unit. (You can choose 1 unit to be 2 cm or 3 cm for a clear drawing). -
Step 2: Constructing &&\sqrt{2}&&
At point &&P_1&&, use your protractor to draw a line segment &&P_1P_2&& of length &&1&& unit that is perpendicular to &&OP_1&&. Now, join &&O&& to &&P_2&&. You have a right-angled triangle &&\triangle OP_1P_2&&. The hypotenuse &&OP_2&& has a length of:
&&OP_2 = \sqrt{OP_1^2 + P_1P_2^2} = \sqrt{1^2 + 1^2} = \sqrt{2}&& -
Step 3: Constructing &&\sqrt{3}&&
Now, use the hypotenuse &&OP_2&& as your new base. At point &&P_2&&, draw a new perpendicular line segment &&P_2P_3&& of length &&1&& unit. Join &&O&& to &&P_3&&. In the new right-angled triangle &&\triangle OP_2P_3&&, the hypotenuse &&OP_3&& has a length of:
&&OP_3 = \sqrt{OP_2^2 + P_2P_3^2} = \sqrt{(\sqrt{2})^2 + 1^2} = \sqrt{2 + 1} = \sqrt{3}&& -
Step 4: Constructing &&\sqrt{4}&& (or &&2&&)
Repeat the process. At point &&P_3&&, draw a perpendicular line segment &&P_3P_4&& of length &&1&& unit. Join &&O&& to &&P_4&&. The hypotenuse &&OP_4&& of &&\triangle OP_3P_4&& will have a length of:
&&OP_4 = \sqrt{OP_3^2 + P_3P_4^2} = \sqrt{(\sqrt{3})^2 + 1^2} = \sqrt{3 + 1} = \sqrt{4} = 2&&
You can check this! The length of &&OP_4&& should be exactly double your starting unit length. -
Step 5: Continue the Spiral
Continue this process. For any point &&P_n&&, you draw a perpendicular segment &&P_nP_{n+1}&& of length &&1&& unit and join &&O&& to &&P_{n+1}&&. The length of &&OP_{n+1}&& will be &&\sqrt{n+1}&&. As you keep going, you will see a beautiful spiral taking shape.
Conclusion and Key Points ✅
This activity is a fantastic way to see a mathematical concept come to life. The key takeaways from these ncert solutions for this activity are:
- The square root spiral is a visual proof of the existence of irrational lengths.
- It is built upon the repeated and sequential application of the Pythagoras theorem.
- The length from the origin &&O&& to any point &&P_n&& on the spiral is exactly &&\sqrt{n}&&.
- Start with a line segment of &&1&& unit.
- The new segment you add at each step must be &&1&& unit long and perpendicular to the previous hypotenuse.
- Accuracy is key! Use a protractor for the &&90^\circ&& angles to get a perfect spiral.
FAQ
Q: What is the purpose of the square root spiral activity?
A: The purpose of the square root spiral is to provide a visual and geometric representation of the square roots of positive integers (like &&\sqrt{2}, \sqrt{3}$$, etc.) and to offer a hands-on demonstration of the repeated application of the Pythagoras theorem.
Q: What mathematical theorem is this activity based on?
A: The entire activity is based on the Pythagoras theorem, which states that in a right-angled triangle with sides ‘a’ and ‘b’ and hypotenuse ‘c’, the relationship is &&a^2 + b^2 = c^2&&.
Q: What will be the length of the line segment &&OP_5&& in the spiral?
A: Following the construction pattern, the length of the hypotenuse &&OP_n&& is always &&\sqrt{n}&&. Therefore, the length of the line segment &&OP_5&& will be exactly &&\sqrt{5}&& units.
Q: Is the length of each small perpendicular line always 1 unit?
A: Yes, for the standard construction of the square root spiral as described in the NCERT textbook, the perpendicular height added at each step is always &&1&& unit.
Q: How many steps can I continue this process for?
A: Theoretically, the process can be continued forever. Practically, you can continue it for as many steps as you can fit on your sheet of paper before the lines become too crowded to draw accurately.
Further Reading
For more fun activities and a deeper understanding of number systems, you can refer to the official NCERT textbooks.

