NCERT Solutions for Class 9 Maths Exercise 1.4 Question 4

Understanding the Question 🧐
The goal of this question is to locate the position of the irrational number &&\sqrt{9.3}&& on the number line. Since we cannot measure this length directly, we will use a geometric construction method that relies on circles and the Pythagorean theorem to find the exact length and then transfer it to our number line.
Represent &&\sqrt{9.3}&& on the number line.
Steps of Construction 📝
Here are the step-by-step instructions to construct &&\sqrt{9.3}&&. You will need a ruler, compass, and pencil.
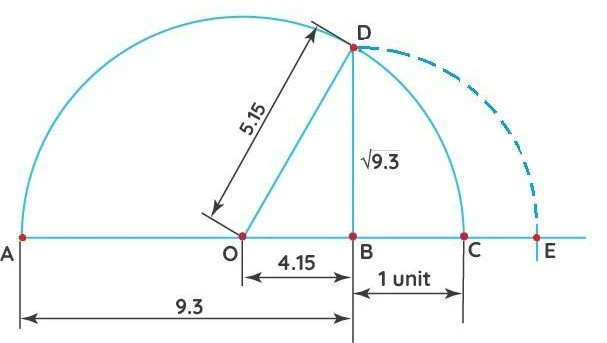
- Draw the Base Line: Draw a line segment &&AB = 9.3&& units.
- Extend the Line: Extend this line from point &&B&& to a new point &&C&& such that the length of &&BC = 1&& unit. The total length of &&AC&& is now &&9.3 + 1 = 10.3&& units.
- Find the Midpoint: Find the midpoint of the segment &&AC&&. Let’s call this midpoint &&O&&. (You can do this by constructing the perpendicular bisector of &&AC&&).
- Draw a Semicircle: With &&O&& as the center and &&OA&& (or &&OC&&) as the radius, draw a semicircle that starts at &&A&& and ends at &&C&&.
- Draw a Perpendicular: At point &&B&&, draw a line that is perpendicular to &&AC&&. Extend this perpendicular line until it intersects the semicircle at a point. Let’s call this point &&D&&.
- The Required Length: The length of the line segment &&BD&& is exactly &&\sqrt{9.3}&&.
- Transfer to Number Line: To plot this on the number line, consider the line &&AC&& as your number line, with point &&B&& as the origin (&&0&&). Place the tip of your compass at &&B&& and the pencil tip at &&D&&.
- Mark the Point: Draw an arc with radius &&BD&& that intersects the number line. Let’s call this intersection point &&E&&. Point &&E&& is the representation of &&\sqrt{9.3}&& on the number line.
Proof: Why This Method Works 🤔
Let’s use the Pythagorean theorem to prove that the length of &&BD&& is indeed &&\sqrt{9.3}&&.
Consider the right-angled triangle &&\Delta OBD&& (since &&BD&& is perpendicular to &&AC&&).
- Finding the Hypotenuse (&&OD&&): &&OD&& is the radius of the semicircle. The diameter is &&AC = 9.3 + 1 = 10.3&& units. Therefore, the radius is:
&&OD = \frac{AC}{2} = \frac{10.3}{2} = 5.15&& units. - Finding the Base (&&OB&&): The length of &&OB&& can be found by subtracting &&BC&& from the radius &&OC&&.
&&OB = OC – BC = 5.15 – 1 = 4.15&& units. - Applying Pythagoras Theorem: In &&\Delta OBD&&, we have:
&&OD^2 = OB^2 + BD^2&&
&&BD^2 = OD^2 – OB^2&&
&&BD^2 = (5.15)^2 – (4.15)^2&& - Simplifying using &&a^2 – b^2 = (a-b)(a+b)&&:
&&BD^2 = (5.15 – 4.15)(5.15 + 4.15)&&
&&BD^2 = (1)(9.3)&&
&&BD^2 = 9.3&& - Final Result:
&&BD = \sqrt{9.3}&&
This proves that our construction is mathematically correct.
- Draw line segment &&AB = x&& (here, &&x = 9.3&&).
- Extend to &&C&& such that &&BC = 1&&.
- Find the midpoint &&O&& of &&AC&&.
- Draw a semicircle with center &&O&& and radius &&OA&&.
- Draw a perpendicular from &&B&& to intersect the semicircle at &&D&&.
- The length &&BD&& is your answer, &&\sqrt{x}&&.
FAQ ❓
Q: Why do we add 1 unit to the initial line segment in this construction?
A: Adding 1 unit helps create a semicircle with a diameter of &&x+1&&. This setup is crucial because it allows us to form a right-angled triangle where the Pythagorean theorem can be used to isolate and find the length &&\sqrt{x}&&.
Q: Can this method be used to represent &&\sqrt{11.5}&& on the number line?
A: Yes, this is a general method. You would simply start with a line segment of &&11.5&& units, extend it by &&1&& unit, and follow the exact same construction steps.
Q: How do you transfer the length of &&\sqrt{9.3}&& to the number line?
A: After constructing the length &&BD = \sqrt{9.3}&&, you treat point &&B&& as the origin (&&0&&). Use a compass with its point at &&B&& and radius set to the length of &&BD&&. The arc you draw will intersect the number line at the exact location of &&\sqrt{9.3}&&.
Further Reading 📖
For more practice with geometric constructions, you can refer to the official NCERT textbook for Class 9 Maths. More resources are available on the NCERT website at https://ncert.nic.in/.


