NCERT Solutions for Class 9 Maths Exercise 3.1 Question 2

Understanding the Question 🧐
This question asks us to create a model of a city’s street plan and then use a given convention to locate specific intersections, known as cross-streets. It’s a great practical example of coordinate geometry. Let’s explore these ncert solutions step-by-step.
(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All the other streets of the city run parallel to these roads and are &&200&& m apart. There are &&5&& streets in each direction. Using &&1\text{cm} = 200\text{m}&&, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the &&2^{\text{nd}}&& street running in the North-South direction and &&5^{\text{th}}&& in the East-West direction meet at some crossing, then we will call this cross-street &&(2, 5)&&. Using this convention, find:
(i) how many cross-streets can be referred to as &&(4, 3)&&.
(ii) how many cross-streets can be referred to as &&(3, 4)&&.
First, let’s visualize and draw the street plan as described. We have:
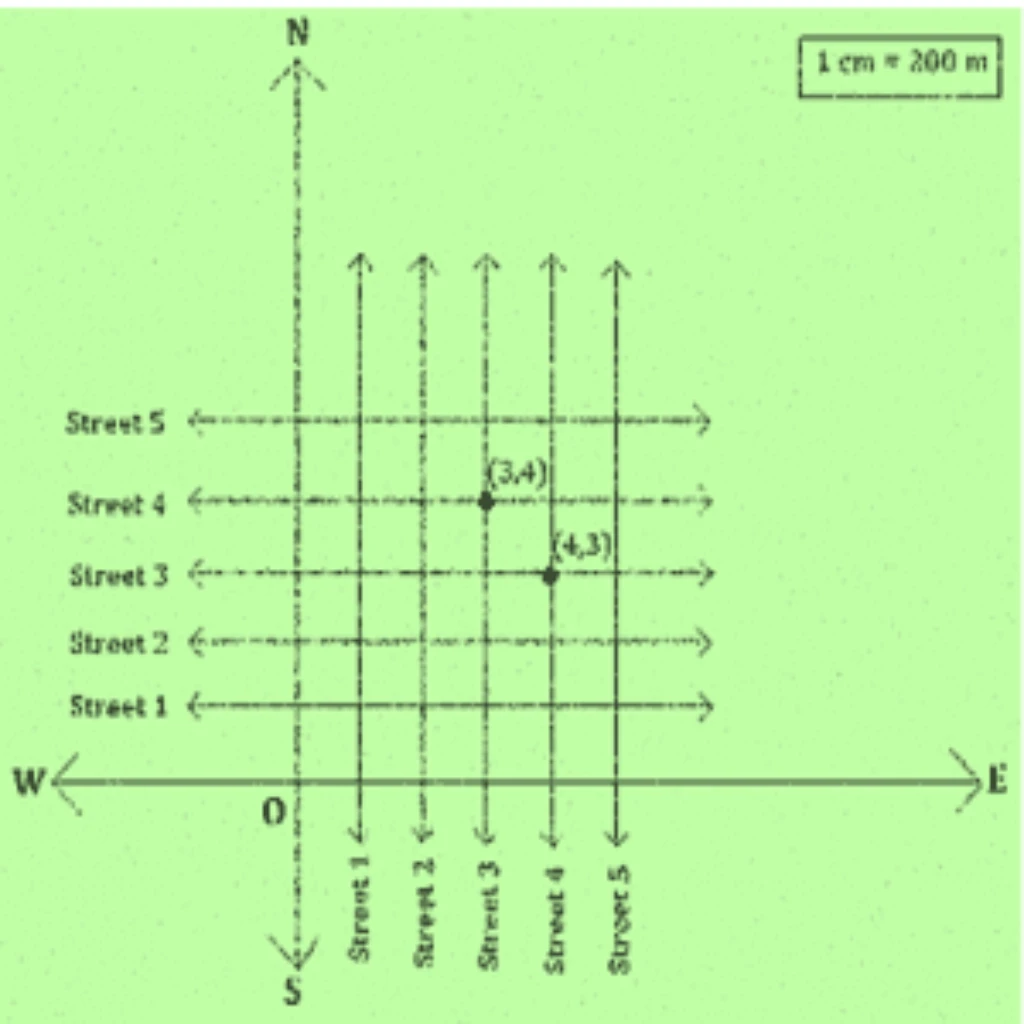
- A main North-South (N-S) road (like a y-axis).
- A main East-West (E-W) road (like an x-axis).
- &&5&& parallel streets in the N-S direction.
- &&5&& parallel streets in the E-W direction.
The convention for naming a cross-street is &&(\text{North-South street number, East-West street number})&&.
Part (i): How many cross-streets can be referred to as &&(4, 3)&& 📝
To find the cross-street &&(4, 3)&&, we need to locate the intersection of:
- The &&4^{\text{th}}&& street running in the North-South direction.
- The &&3^{\text{rd}}&& street running in the East-West direction.
Since each street is a unique straight line, the &&4^{\text{th}}&& N-S street is a single line, and the &&3^{\text{rd}}&& E-W street is also a single line. A fundamental rule in geometry is that two distinct straight lines can intersect at only one point.
Therefore, there is only one unique point where these two specific streets will cross.
Conclusion: Only one cross-street can be referred to as &&(4, 3)&&.
Part (ii): How many cross-streets can be referred to as &&(3, 4)&& 📝
Similarly, to find the cross-street &&(3, 4)&&, we need to locate the intersection of:
- The &&3^{\text{rd}}&& street running in the North-South direction.
- The &&4^{\text{th}}&& street running in the East-West direction.
Just like in the first part, we are dealing with two unique, intersecting straight lines. The &&3^{\text{rd}}&& N-S street and the &&4^{\text{th}}&& E-W street will meet at exactly one point.
Conclusion: Only one cross-street can be referred to as &&(3, 4)&&.
Conclusion and Key Points ✅
This problem beautifully illustrates the core idea of coordinate geometry. Each pair of coordinates, like &&(4, 3)&& or &&(3, 4)&&, corresponds to a single, unique location on a plane. The order matters, as &&(4, 3)&& and &&(3, 4)&& are two different intersections in our city model.
- In coordinate geometry, the order of the numbers in a pair is crucial. &&(a, b)&& is not the same as &&(b, a)&& unless &&a = b&&.
- Two distinct straight lines can intersect at a maximum of one point.
- This street plan is a real-world model of the Cartesian coordinate system, with streets acting as grid lines.
FAQ
Q: What does the cross-street notation &&(2, 5)&& mean in this problem?
A: It refers to the unique intersection point of the &&2^{\text{nd}}&& street running North-South and the &&5^{\text{th}}&& street running East-West.
Q: How many cross-streets can be called &&(4, 3)&&?
A: Only one. The &&4^{\text{th}}&& North-South street and the &&3^{\text{rd}}&& East-West street are unique lines that can intersect at only a single point.
Q: Is the cross-street &&(4, 3)&& the same as &&(3, 4)&&?
A: No, they represent two different and unique intersection points. &&(4, 3)&& is the crossing of the &&4^{\text{th}}&& N-S street and &&3^{\text{rd}}&& E-W street, while &&(3, 4)&& is the crossing of the &&3^{\text{rd}}&& N-S street and &&4^{\text{th}}&& E-W street.
Q: What is the main concept demonstrated in this street plan problem?
A: This problem is a practical application of the Cartesian coordinate system. It shows that a unique pair of coordinates specifies a unique location on a plane.
Q: Why is there only one answer for each sub-question?
A: Because two distinct straight lines, like the streets in the model, can intersect at one and only one point. Each street is a unique line, so their intersection point is also unique.
Further Reading
To understand the fundamentals of Coordinate Geometry better, you can refer to the official NCERT textbook provided by the National Council of Educational Research and Training. Visit the NCERT official website for more resources.

