NCERT Solutions for Class 9 Maths Exercise 3.2 Question 2

Understanding the Question 🧐
This question asks us to observe a Cartesian plane graph and identify various points and their coordinates. This is a fundamental skill in coordinate geometry. We will use the provided figure to answer eight different sub-questions. These ncert solutions will guide you through each part step-by-step.
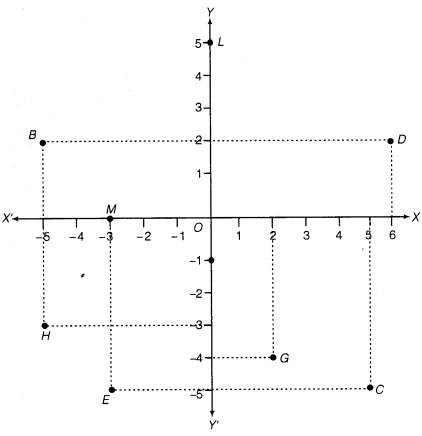
See Fig.3.14, and write the following:
 L, M”>
L, M”>
- The coordinates of B.
- The coordinates of C.
- The point identified by the coordinates (–3, –5).
- The point identified by the coordinates (2, –4).
- The abscissa of the point D.
- The ordinate of the point H.
- The coordinates of the point L.
- The coordinates of the point M.
Part (i): The coordinates of B 📝
To find the coordinates of point B, we need to find its distance from the y-axis (which gives the x-coordinate) and its distance from the x-axis (which gives the y-coordinate).
- The perpendicular distance of B from the y-axis is 5 units to the left, so the x-coordinate (abscissa) is &&-5&&.
- The perpendicular distance of B from the x-axis is 2 units upwards, so the y-coordinate (ordinate) is &&2&&.
Therefore, the coordinates of point B are &&(-5, 2)&&.
Part (ii): The coordinates of C 📝
Let’s find the coordinates for point C using the same method.
- The perpendicular distance of C from the y-axis is 5 units to the right, so the x-coordinate is &&5&&.
- The perpendicular distance of C from the x-axis is 5 units downwards, so the y-coordinate is &&-5&&.
Therefore, the coordinates of point C are &&(5, -5)&&.
Part (iii): The point identified by the coordinates &&(-3, -5)&& 📝
Here, we are given the coordinates and need to find the point. The coordinates are &&(x, y) = (-3, -5)&&.
- An x-coordinate of &&-3&& means we move 3 units to the left of the origin.
- A y-coordinate of &&-5&& means we move 5 units down from the x-axis.
Looking at the graph, the point that matches this position is E.
Part (iv): The point identified by the coordinates &&(2, -4)&& 📝
The coordinates are &&(x, y) = (2, -4)&&.
- An x-coordinate of &&2&& means we move 2 units to the right of the origin.
- A y-coordinate of &&-4&& means we move 4 units down from the x-axis.
The point at this location on the graph is G.
Part (v): The abscissa of the point D 📝
The ‘abscissa’ is just another name for the x-coordinate. First, let’s find the coordinates of point D.
- Point D is &&6&& units to the right of the y-axis and &&2&& units above the x-axis.
- So, the coordinates of D are &&(6, 2)&&.
The abscissa (x-coordinate) of point D is &&6&&.
Part (vi): The ordinate of the point H 📝
The ‘ordinate’ is another name for the y-coordinate. Let’s find the coordinates of point H first.
- Point H is &&5&& units to the left of the y-axis and &&3&& units below the x-axis.
- So, the coordinates of H are &&(-5, -3)&&.
The ordinate (y-coordinate) of point H is &&-3&&.
Part (vii): The coordinates of the point L 📝
Point L lies directly on the y-axis.
- Any point on the y-axis has an x-coordinate of &&0&&.
- Point L is &&5&& units above the origin.
Therefore, the coordinates of point L are &&(0, 5)&&.
Part (viii): The coordinates of the point M 📝
Point M lies directly on the x-axis.
- Any point on the x-axis has a y-coordinate of &&0&&.
- Point M is &&3&& units to the left of the origin.
Therefore, the coordinates of point M are &&(-3, 0)&&.
Conclusion and Key Points ✅
By carefully observing the graph, we have successfully identified the coordinates and points as requested. The key is to remember that a coordinate pair &&(x, y)&& represents the horizontal distance &&(x)&& followed by the vertical distance &&(y)&& from the origin.
- The x-coordinate is called the abscissa.
- The y-coordinate is called the ordinate.
- The coordinates of the origin are &&(0, 0)&&.
- For any point on the x-axis, the y-coordinate is &&0&&. Example: &&(x, 0)&&.
- For any point on the y-axis, the x-coordinate is &&0&&. Example: &&(0, y)&&.
FAQ
Q: What are the coordinates of point B in the given figure?
A: To find the coordinates of point B, we look at its position relative to the x-axis and y-axis. The x-coordinate (abscissa) is &&-5&& and the y-coordinate (ordinate) is &&2&&. So, the coordinates of point B are &&(-5, 2)&&.
Q: What is the abscissa of point D?
A: The abscissa is another name for the x-coordinate of a point. For point D, the coordinates are &&(6, 2)&&. Therefore, the abscissa of point D is &&6&&.
Q: What is the ordinate of point H?
A: The ordinate is another name for the y-coordinate of a point. For point H, the coordinates are &&(-5, -3)&&. Therefore, the ordinate of point H is &&-3&&.
Q: Which point is identified by the coordinates &&(-3, -5)&&?
A: To find the point for coordinates &&(-3, -5)&&, we start at the origin, move &&3&& units to the left on the x-axis (to &&x = -3&&), and then &&5&& units down parallel to the y-axis (to &&y = -5&&). The point located at this position is E.
Q: What are the coordinates of point L and M?
A: Point L lies on the y-axis at a distance of &&5&& units above the origin, so its x-coordinate is &&0&&. Its coordinates are &&(0, 5)&&. Point M lies on the x-axis at a distance of &&3&& units to the left of the origin, so its y-coordinate is &&0&&. Its coordinates are &&(-3, 0)&&.
Further Reading
For a deeper understanding of Coordinate Geometry, you can refer to the official NCERT textbook for Class 9 Maths. Download the book from the official website: https://ncert.nic.in/.


