NCERT Solutions for Class 9 Maths Exercise 5.1 Question 1
Understanding the Question 🧐
This question asks us to check several statements related to basic geometry and decide if they are true or false. We need to use Euclid’s definitions, postulates, and axioms to justify our answers. These are the fundamental rules of geometry that we accept without proof. Understanding these rules is essential for mastering this chapter. Let’s dive into these ncert solutions and break down each statement step-by-step.
Which of the following statements are true and which are false? Give reasons for your answers.
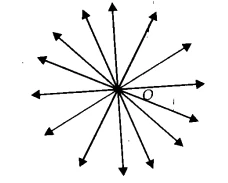
Part (i): Only one line can pass through a single point. 📝
Statement: “Only one line can pass through a single point.”
Answer: False
Reason: Through a single point, we can draw an infinite number of lines. Think of a point as the center of a wheel. You can draw countless lines (like spokes) that all pass through that center point. To define a unique line, we need two distinct points, not just one.
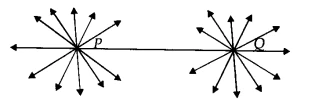
Part (ii): There are an infinite number of lines which pass through two distinct points. 📝
Statement: “There are an infinite number of lines which pass through two distinct points.”
Answer: False
Reason: This statement contradicts Euclid’s Axiom 5.1. The axiom states: ‘Given two distinct points, there is a unique line that passes through them.’ If you have two points, say A and B, you can only draw one single straight line that connects both of them. You cannot draw multiple different straight lines through the same two points.
Part (iii): A terminated line can be produced indefinitely on both the sides. 📝
Statement: “A terminated line can be produced indefinitely on both the sides.”
Answer: True
Reason: This is a direct statement of one of Euclid’s Postulates (Postulate 2). In modern terms, a “terminated line” is what we call a line segment. The postulate tells us that any line segment can be extended forever in a straight line in both directions. This is the very concept that turns a line segment into a line.
Part (iv): If two circles are equal, then their radii are equal. 📝
Statement: “If two circles are equal, then their radii are equal.”
Answer: True
Reason: When we say two circles are “equal,” we mean they are congruent. This means if you place one circle on top of the other, they will overlap perfectly. Their boundaries (circumferences) will coincide. This is only possible if the distance from the center to any point on the boundary, which is the radius, is the same for both circles.

Part (v): In Fig. 5.9, if &&AB = PQ&& and &&PQ = XY&&, then &&AB = XY&&. 📝
Statement: “If &&AB = PQ&& and &&PQ = XY&&, then &&AB = XY&&.”
Answer: True
Reason: This statement is a perfect example of Euclid’s first axiom, which states: ‘Things which are equal to the same thing are equal to one another.’ Here, the line segment &&AB&& is equal to &&PQ&&. The line segment &&XY&& is also equal to &&PQ&&. Since both &&AB&& and &&XY&& are equal to the same thing (&&PQ&&), they must be equal to each other. Therefore, &&AB = XY&&.
Conclusion and Key Points ✅
This question tests our understanding of the fundamental building blocks of geometry. By analyzing each statement, we have applied several of Euclid’s key axioms and postulates. The main takeaway is that geometry is built on a logical system of rules that cannot be broken. Always refer back to these basic definitions when you are in doubt!
Axioms are for All of mathematics (like algebra and geometry).
Postulates are Particular to geometry.
- An infinite number of lines can pass through one point.
- Only one unique line can pass through two distinct points.
- A line segment (terminated line) can be extended indefinitely to form a line.
- If two figures (like circles) are equal (congruent), their corresponding parts (like radii) are also equal.
- The axiom ‘Things which are equal to the same thing are equal to one another’ is a powerful tool for proving equality. (e.g., if &&a=b&& and &&b=c&&, then &&a=c&&).
FAQ
Q: Is the statement ‘Only one line can pass through a single point’ true or false?
A: The statement is false. An infinite number of lines can pass through a single point. Think of the spokes of a wheel all passing through the center point.
Q: Why can only one line pass through two distinct points?
A: This is based on Euclid’s axiom which states that ‘Given two distinct points, there is a unique line that passes through them’. You can’t draw two different straight lines that connect the same two points.
Q: What is a ‘terminated line’ in Euclidean geometry?
A: A ‘terminated line’ is what we now call a line segment. Euclid’s Postulate 2 states that a terminated line can be produced (extended) indefinitely in both directions to form a line.
Q: How are equal circles and their radii related?
A: If two circles are equal, it means their areas and circumferences are the same, and they can perfectly overlap (superimpose) each other. This is only possible if their central points coincide and their radii are equal.
Q: Which of Euclid’s axioms is used to prove that if &&AB = PQ&& and &&PQ = XY&&, then &&AB = XY&&?
A: This is a direct application of Euclid’s first axiom: ‘Things which are equal to the same thing are equal to one another’. Here, both &&AB&& and &&XY&& are equal to &&PQ&&, so they must be equal to each other.
Further Reading
For more information on Euclid’s Geometry and to access the official Class 9 Maths textbook, you can visit the NCERT website: https://ncert.nic.in/. These foundational concepts are crucial for higher-level mathematics.


