NCERT Solutions for Class 9 Maths Exercise 6.1 Question 6

Hello, students! Welcome to the solution for the final question of Exercise 6.1. This problem is an excellent test of your understanding of the linear pair axiom and the properties of an angle bisector. A key part of this question is drawing the figure correctly from the description.
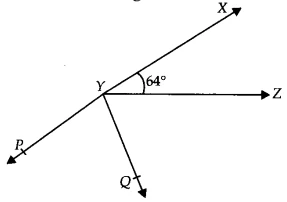
| Given Information | &&\angle XYZ = 64^\circ&&, line XY is produced to point P, and ray YQ bisects &&\angle ZYP&&. |
|---|---|
| What to Find | The measures of &&\angle XYQ&& and reflex &&\angle QYP&&. |
| Final Answer | &&\angle XYQ = 122^\circ&& and reflex &&\angle QYP = 302^\circ&&. |
Question 6: It is given that &&\angle XYZ = 64^\circ&& and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects &&\angle ZYP&&, find &&\angle XYQ&& and reflex &&\angle QYP&&.
How to Find &&\angle XYQ&& and Reflex &&\angle QYP&& 🤔
Follow these four simple steps to construct the figure and find the required angles.
- Step 1: Draw the Figure and Find &&\angle ZYP&&
First, draw a straight line XYP. From point Y, draw a ray YZ such that &&\angle XYZ = 64^\circ&&. Since XYP is a straight line, &&\angle XYZ&& and &&\angle ZYP&& form a linear pair. Calculate &&\angle ZYP = 180^\circ – 64^\circ = 116^\circ&&. - Step 2: Use the Angle Bisector Property
It’s given that ray YQ bisects &&\angle ZYP&&. This means &&\angle ZYP&& is divided into two equal halves, &&\angle ZYQ&& and &&\angle QYP&&. Calculate the measure of these angles: &&\angle QYP = \angle ZYQ = \frac{116^\circ}{2} = 58^\circ&&. - Step 3: Calculate &&\angle XYQ&&
The angle &&\angle XYQ&& is the sum of two adjacent angles, &&\angle XYZ&& and &&\angle ZYQ&&. Add their values: &&\angle XYQ = 64^\circ + 58^\circ = 122^\circ&&. - Step 4: Calculate Reflex &&\angle QYP&&
The reflex of an angle is its measure subtracted from &&360^\circ&&. Calculate the reflex of &&\angle QYP&&: Reflex &&\angle QYP = 360^\circ – 58^\circ = 302^\circ&&.
Detailed Step-by-Step Solution 📝
First, let’s draw the figure as described in the question.
Here, XYP is a straight line, &&\angle XYZ = 64^\circ&&, and ray YQ bisects &&\angle ZYP&&.
Step 1: Find &&\angle ZYP&&
Since XYP is a straight line, the angles &&\angle XYZ&& and &&\angle ZYP&& form a linear pair.
&&\implies \angle XYZ + \angle ZYP = 180^\circ&&
Substitute the given value of &&\angle XYZ&&:
&&64^\circ + \angle ZYP = 180^\circ&&
&&\angle ZYP = 180^\circ – 64^\circ = 116^\circ&&
Step 2: Find &&\angle ZYQ&& and &&\angle QYP&&
We are given that ray YQ bisects &&\angle ZYP&&. This means it divides the angle into two equal parts.
&&\angle ZYQ = \angle QYP = \frac{1}{2} \angle ZYP&&
&&\implies \angle QYP = \frac{116^\circ}{2} = 58^\circ&&
So, &&\angle ZYQ = 58^\circ&& and &&\angle QYP = 58^\circ&&.
Step 3: Find &&\angle XYQ&&
From the figure, it is clear that &&\angle XYQ&& is the sum of &&\angle XYZ&& and &&\angle ZYQ&&.
&&\angle XYQ = \angle XYZ + \angle ZYQ&&
&&\angle XYQ = 64^\circ + 58^\circ&&
&&\angle XYQ = 122^\circ&&
Step 4: Find reflex &&\angle QYP&&
The reflex of an angle is calculated by subtracting its measure from &&360^\circ&&.
Reflex &&\angle QYP = 360^\circ – \angle QYP&&
Reflex &&\angle QYP = 360^\circ – 58^\circ&&
Reflex &&\angle QYP = 302^\circ&&
Key Concepts Used ✅
- Linear Pair Axiom: Angles on a straight line add up to &&180^\circ&&.
- Angle Bisector: A ray that divides an angle into two equal parts.
- Reflex Angle: The angle measured on the outside, calculated as &&360^\circ – \text{angle}&&.
Common Mistakes to Avoid 🖍️
A common error is to misinterpret the diagram. Make sure to draw the figure accurately first. Another mistake is forgetting to calculate the reflex angle for &&\angle QYP&& and only providing the value &&58^\circ&&. Always read the question carefully to ensure you answer all parts.
FAQ (Frequently Asked Questions)
Q: What is the first step in solving this problem?
A: The first and most crucial step is to draw an accurate figure based on the given information. Draw a straight line XYP, an angle &&\angle XYZ = 64^\circ&&, and a ray YQ that bisects &&\angle ZYP&&.
Q: What does ‘angle bisector’ mean?
A: An angle bisector is a ray that divides an angle into two exactly equal angles. In this problem, YQ bisects &&\angle ZYP&&, so &&\angle ZYQ = \angle QYP&&.
Q: How is the value of &&\angle ZYP&& found?
A: Since XYP is a straight line, the angles &&\angle XYZ&& and &&\angle ZYP&& form a linear pair, meaning their sum is &&180^\circ&&. We find &&\angle ZYP&& by subtracting the given angle from &&180^\circ&&: &&\angle ZYP = 180^\circ – 64^\circ = 116^\circ&&.
Q: How do you calculate a reflex angle?
A: A reflex angle is the angle that is greater than &&180^\circ&& but less than &&360^\circ&&. To calculate it, you subtract the measure of the original angle from &&360^\circ&&. In this case, Reflex &&\angle QYP = 360^\circ – 58^\circ = 302^\circ&&.
Further Reading
To master the concepts used in this exercise, practice more problems from your NCERT Class 9 Maths textbook. You can find the official textbook at https://ncert.nic.in/.

