NCERT Solutions for Class 9 Maths Exercise 6.2 Question 3

Understanding the Question 🧐
This problem involves understanding the relationships between angles formed when a transversal line intersects two parallel lines. We are given some information and need to find the measures of three specific angles. This is a classic geometry problem that tests our knowledge of parallel line properties. The official ncert solutions guide us through these properties.
In the given figure, if &&AB || CD&&, &&EF \perp CD&& and &&\angle GED = 126^\circ&&, find &&\angle AGE&&, &&\angle GEF&& and &&\angle FGE&&.
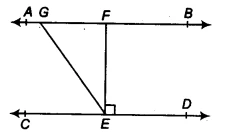
Given Information:
- Line &&AB&& is parallel to line &&CD&& (i.e., &&AB || CD&&).
- Line &&EF&& is perpendicular to line &&CD&& (i.e., &&EF \perp CD&&). This means &&\angle FED = 90^\circ&&.
- The measure of angle &&GED&& is &&126^\circ&&.
To Find:
- &&\angle AGE&&
- &&\angle GEF&&
- &&\angle FGE&&
Part 1: Finding the value of &&\angle AGE&& 📝
To find &&\angle AGE&&, we need to look at its relationship with the given angle &&\angle GED&&.
Step 1: Identify the relationship between the angles.
Since &&AB || CD&& and &&GE&& is the transversal line that intersects them, the angles &&\angle AGE&& and &&\angle GED&& form a pair of alternate interior angles.
Step 2: Apply the Alternate Interior Angles Theorem.
A key property of parallel lines states that alternate interior angles are equal.
Therefore, &&\angle AGE = \angle GED&&.
Step 3: Substitute the given value.
We are given that &&\angle GED = 126^\circ&&.
So, &&\angle AGE = 126^\circ&&.
Part 2: Finding the value of &&\angle GEF&& 📝
Now, let’s find &&\angle GEF&&. Notice that &&\angle GED&& is made up of two smaller angles, &&\angle GEF&& and &&\angle FED&&.
Step 1: Express &&\angle GED&& as a sum of its parts.
From the figure, we can see that: &&\angle GED = \angle GEF + \angle FED&&.
Step 2: Use the information that &&EF \perp CD&&.
We are given that &&EF&& is perpendicular to &&CD&&. This means the angle they form is a right angle.
So, &&\angle FED = 90^\circ&&.
Step 3: Substitute the known values into the equation from Step 1.
We have &&\angle GED = 126^\circ&& and &&\angle FED = 90^\circ&&.
&&126^\circ = \angle GEF + 90^\circ&&
Step 4: Solve for &&\angle GEF&&.
To find &&\angle GEF&&, we subtract &&90^\circ&& from &&126^\circ&&.
&&\angle GEF = 126^\circ – 90^\circ&&
&&\angle GEF = 36^\circ&&.
Part 3: Finding the value of &&\angle FGE&& 📝
Finally, we need to find &&\angle FGE&&. We can find this by using the property of a linear pair of angles on the straight line &&AB&&.
Step 1: Identify the linear pair.
The ray &&GE&& stands on the line &&AB&&. Therefore, &&\angle AGE&& and &&\angle FGE&& form a linear pair.
Step 2: Apply the Linear Pair Axiom.
The sum of angles in a linear pair is always &&180^\circ&&.
So, &&\angle AGE + \angle FGE = 180^\circ&&.
Step 3: Substitute the value of &&\angle AGE&& we found in Part 1.
We already calculated that &&\angle AGE = 126^\circ&&.
&&126^\circ + \angle FGE = 180^\circ&&
Step 4: Solve for &&\angle FGE&&.
Subtract &&126^\circ&& from &&180^\circ&&.
&&\angle FGE = 180^\circ – 126^\circ&&
&&\angle FGE = 54^\circ&&.
Conclusion and Key Points ✅
By applying the fundamental properties of parallel lines and linear pairs, we have successfully found all the required angles.
The final answers are:
- &&\angle AGE = 126^\circ&&
- &&\angle GEF = 36^\circ&&
- &&\angle FGE = 54^\circ&&
- If two parallel lines are intersected by a transversal, then each pair of alternate interior angles is equal.
- If a ray stands on a line, the sum of the adjacent angles so formed (a linear pair) is &&180^\circ&&.
- Perpendicular lines intersect at a right angle (&&90^\circ&&).
Frequently Asked Questions (FAQ)
Q: What are alternate interior angles in this problem?
A: In this problem, &&\angle AGE&& and &&\angle GED&& are alternate interior angles. They are located on opposite sides of the transversal line &&GE&& and are ‘inside’ or between the two parallel lines &&AB&& and &&CD&&.
Q: Why is &&\angle AGE&& equal to &&\angle GED&&?
A: According to the Alternate Interior Angles Theorem, when a transversal intersects two parallel lines, the alternate interior angles formed are equal. Since we are given &&AB || CD&&, it must be that &&\angle AGE = \angle GED&&.
Q: How is the value of &&\angle GEF&& calculated?
A: The angle &&\angle GED&& is made of two parts: &&\angle GEF&& and &&\angle FED&&. We are given &&\angle GED = 126^\circ&&. Since &&EF \perp CD&&, we know &&\angle FED = 90^\circ&&. By subtracting, we get &&\angle GEF = \angle GED – \angle FED = 126^\circ – 90^\circ = 36^\circ&&.
Q: What is a linear pair of angles?
A: A linear pair is a pair of adjacent angles formed when two lines intersect. Their non-common sides are opposite rays (forming a straight line), and their sum is always &&180^\circ&&.
Q: How do we find &&\angle FGE&& using the linear pair axiom?
A: The angles &&\angle AGE&& and &&\angle FGE&& are adjacent angles on the straight line &&AB&&. They form a linear pair, so their sum is &&180^\circ&&. Since we found &&\angle AGE = 126^\circ&&, we can calculate &&\angle FGE&& as &&180^\circ – 126^\circ = 54^\circ&&.
Q: What does the condition &&EF \perp CD&& tell us?
A: The condition &&EF \perp CD&& means that the line segment &&EF&& is perpendicular to the line &&CD&&. This is crucial because it tells us that the angle formed at their intersection, &&\angle FED&&, is a right angle, measuring exactly &&90^\circ&&.
Further Reading
For more details on the properties of lines and angles, you can refer to the official NCERT textbook provided by the National Council of Educational Research and Training. Visit their website at https://ncert.nic.in/ for official resources.


