NCERT Solutions for Class 9 Maths Exercise 7.1 Question 2

Understanding the Question 🧐
This question asks us to prove three separate but related statements about a quadrilateral &&ABCD&&. The key is to first prove that two overlapping triangles within the quadrilateral are congruent. Once we establish their congruence, the other two proofs will follow easily. These ncert solutions will guide you through each part logically.
&&ABCD&& is a quadrilateral in which &&AD = BC&& and &&\angle DAB = \angle CBA&&. Prove that:
(i) &&\triangle ABD \cong \triangle BAC&&
(ii) &&BD = AC&&
(iii) &&\angle ABD = \angle BAC&&
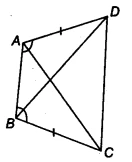
Step-by-Step Solution 📝
Part (i): Prove that &&\triangle ABD \cong \triangle BAC&&
Step 1: Identify the Triangles and Given Information
We need to compare &&\triangle ABD&& and &&\triangle BAC&&. Let’s list what we know from the question:
- Side: &&AD = BC&& (Given)
- Angle: &&\angle DAB = \angle CBA&& (Given)
Step 2: Look for Common Elements
Notice that both triangles share the side &&AB&&. This is a common side.
- Side: &&AB = BA&& (Common side)
Step 3: Apply the Congruence Rule
Let’s assemble the parts we’ve found for &&\triangle ABD&& and &&\triangle BAC&&:
- &&AD = BC&& (Given Side)
- &&\angle DAB = \angle CBA&& (Given Included Angle)
- &&AB = BA&& (Common Side)
We have two sides and the angle included between them. This fits the Side-Angle-Side (SAS) congruence criterion.
Therefore, by the SAS congruence rule:
&&\triangle ABD \cong \triangle BAC&&
Part (ii): Prove that &&BD = AC&&
This part directly follows from the result of Part (i).
Since we have already proven that &&\triangle ABD \cong \triangle BAC&&, we can use the CPCTC theorem.
CPCTC stands for Corresponding Parts of Congruent Triangles are Congruent (or equal).
The side &&BD&& in &&\triangle ABD&& corresponds to the side &&AC&& in &&\triangle BAC&&.
Therefore, by CPCTC:
&&BD = AC&&
Part (iii): Prove that &&\angle ABD = \angle BAC&&
Similar to Part (ii), we use the congruence we proved in Part (i).
Since &&\triangle ABD \cong \triangle BAC&&, their corresponding angles must also be equal by CPCTC.
The angle &&\angle ABD&& in &&\triangle ABD&& corresponds to the angle &&\angle BAC&& in &&\triangle BAC&&.
Therefore, by CPCTC:
&&\angle ABD = \angle BAC&&
Conclusion and Key Points ✅
The entire problem is solved by first establishing the congruence of &&\triangle ABD&& and &&\triangle BAC&& using the SAS rule. Once the congruence is proven, the other two results—that &&BD = AC&& and &&\angle ABD = \angle BAC&&—are straightforward consequences derived from CPCTC.
- The SAS congruence rule requires two sides and the angle included between them to be equal.
- CPCTC is a powerful tool, but it can only be used after you have proven that two triangles are congruent.
- Always start by listing the given information and identifying any common sides or angles.
FAQ (Frequently Asked Questions)
Q: What congruence rule was used to solve this problem?
A: The Side-Angle-Side (SAS) congruence rule was used in Part (i) to prove that &&\triangle ABD \cong \triangle BAC&&.
Q: Why are parts (ii) and (iii) solved after part (i)?
A: Parts (ii) and (iii) are proven using CPCTC (Corresponding Parts of Congruent Triangles are Congruent). This rule can only be applied after the congruence of the triangles has been established, which was done in Part (i).
Q: How do we identify corresponding parts for CPCTC?
A: Corresponding parts are in the same position in the names of the congruent triangles. For &&\triangle ABD \cong \triangle BAC&&, the side &&BD&& (last two letters) corresponds to &&AC&& (last two letters), and the angle &&\angle ABD&& corresponds to the angle &&\angle BAC&&.
Q: What does CPCTC stand for?
A: CPCTC stands for ‘Corresponding Parts of Congruent Triangles are Congruent’. It’s a fundamental theorem used to show that if two triangles are congruent, then all their corresponding sides and angles are equal.
Q: What were the three conditions used for the SAS rule in this proof?
A: The three conditions were:
1. &&AD = BC&& (Given Side)
2. &&\angle DAB = \angle CBA&& (Given Included Angle)
3. &&AB = BA&& (Common Side)
Further Reading
For a deeper understanding of triangle congruence, you can refer to the official NCERT Class 9 Mathematics textbook on their website: https://ncert.nic.in/.


