NCERT Solutions for Class 9 Maths Exercise 7.3 Question 2

Welcome, students! Let’s walk through the solution for Question 2 of Exercise 7.3. This problem proves a very important property of isosceles triangles using the RHS congruence rule. Understanding this proof will strengthen your geometry skills.
| Given Information | An isosceles triangle &&\triangle ABC&& with &&AB = AC&&, and AD is an altitude to BC (&&AD \perp BC&&). |
|---|---|
| To Prove | (i) AD bisects BC (&&BD = CD&&) (ii) AD bisects &&\angle A&& (&&\angle BAD = \angle CAD&&) |
| Key Concept Used | RHS (Right angle-Hypotenuse-Side) congruence rule. |
Question 2: AD is an altitude of an isosceles triangle ABC in which &&AB = AC&&. Show that (i) AD bisects BC (ii) AD bisects &&\angle A&&.
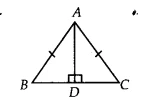
How to Prove the Properties of the Altitude 🤔
This proof can be completed in four logical steps by proving the two smaller triangles are congruent.
- Step 1: Identify the Triangles to Prove Congruent
The altitude AD from vertex A to the base BC divides the isosceles triangle ABC into two right-angled triangles: &&\triangle ABD&& and &&\triangle ACD&&. The proof relies on showing that these two triangles are congruent. - Step 2: List the Known Equal Parts for RHS Congruence
Compare the two triangles, &&\triangle ABD&& and &&\triangle ACD&&. We can identify three equal parts that match the RHS criteria:- Right Angle (R): &&\angle ADB = \angle ADC&& (both are &&90^\circ&& because AD is an altitude).
- Hypotenuse (H): &&AB = AC&& (given, as &&\triangle ABC&& is isosceles).
- Side (S): &&AD = AD&& (this side is common to both triangles).
- Step 3: Apply the RHS Congruence Rule
Since the right angle, hypotenuse, and one corresponding side of &&\triangle ABD&& are equal to those of &&\triangle ACD&&, we can conclude that the triangles are congruent by the RHS (Right angle-Hypotenuse-Side) congruence rule. So, &&\triangle ABD \cong \triangle ACD&&. - Step 4: Use CPCTC to Prove Both Parts of the Question
Now that the triangles are congruent, their corresponding parts are equal (CPCTC).- For Part (i), the corresponding sides &&BD&& and &&CD&& are equal, which means AD bisects BC.
- For Part (ii), the corresponding angles &&\angle BAD&& and &&\angle CAD&& are equal, which means AD bisects &&\angle A&&.
Detailed Step-by-Step Proof 📝
Here is the formal proof, broken down into the two parts required by the question.
Given:
&&\triangle ABC&& is an isosceles triangle where &&AB = AC&&.
AD is an altitude to BC, which means &&AD \perp BC&& and &&\angle ADB = \angle ADC = 90^\circ&&.
First, we will prove that &&\triangle ABD&& and &&\triangle ACD&& are congruent.
In &&\triangle ABD&& and &&\triangle ACD&&:
- &&\angle ADB = \angle ADC&& (Each &&90^\circ&&, as AD is an altitude) [R]
- &&AB = AC&& (Given, this is the hypotenuse) [H]
- &&AD = AD&& (Common side) [S]
Therefore, by the RHS congruence rule, we have:
&&\triangle ABD \cong \triangle ACD&&
Now, we can prove the two parts of the question using CPCTC (Corresponding Parts of Congruent Triangles are equal).
(i) AD bisects BC
Since &&\triangle ABD \cong \triangle ACD&&, their corresponding sides must be equal.
&&\implies BD = CD&& (by CPCTC)
If &&BD = CD&&, it means D is the midpoint of BC.
Therefore, AD bisects BC.
(ii) AD bisects &&\angle A&&
Since &&\triangle ABD \cong \triangle ACD&&, their corresponding angles must be equal.
&&\implies \angle BAD = \angle CAD&& (by CPCTC)
If &&\angle BAD = \angle CAD&&, it means AD divides &&\angle A&& into two equal parts.
Therefore, AD bisects &&\angle A&&.
Key Property of Isosceles Triangles ✅
This question proves a very important property you should remember: In an isosceles triangle, the altitude from the vertex angle (the angle between the equal sides) to the base is also the median to the base and the bisector of the vertex angle.
FAQ (Frequently Asked Questions)
Q: What is the RHS congruence rule?
A: The RHS (Right angle-Hypotenuse-Side) congruence rule is a special case for right-angled triangles. It states that if the hypotenuse and one side of a right-angled triangle are equal to the hypotenuse and one corresponding side of another right-angled triangle, then the two triangles are congruent.
Q: What is the difference between an altitude and a median?
A: An altitude is a line from a vertex that is perpendicular (at &&90^\circ&&) to the opposite side. A median is a line from a vertex to the midpoint of the opposite side. This problem proves that in an isosceles triangle, the altitude from the vertex angle is also a median.
Q: Why is AB the hypotenuse?
A: The hypotenuse is always the side opposite the right angle in a right-angled triangle. In &&\triangle ABD&&, the right angle is &&\angle ADB&&, and the side opposite to it is &&AB&&. Similarly, in &&\triangle ACD&&, &&AC&& is the hypotenuse.
Q: What important property of isosceles triangles does this question prove?
A: This question proves a key property: in an isosceles triangle, the altitude drawn from the vertex angle (the angle between the equal sides) to the base is also the median to the base and the bisector of the vertex angle.


