NCERT Solutions for Class 9 Maths Exercise 8.1 Question 2

Welcome to the solution for Question 2 of Exercise 8.1. This is a classic proof problem where we use the properties of a parallelogram and triangle congruence to show that if a parallelogram has equal diagonals, it must be a rectangle.
| Given Information | A parallelogram ABCD where the diagonals are equal (&&AC = BD&&). |
|---|---|
| To Prove | ABCD is a rectangle. |
| Key Concept Used | SSS congruence rule and properties of parallel lines. |
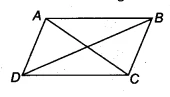
Question 2: If the diagonals of a parallelogram are equal, then show that it is a rectangle.
How to Prove the Parallelogram is a Rectangle 🤔
This proof can be completed in a few logical steps by proving two overlapping triangles are congruent.
- Step 1: State the Given Information and Draw a Figure
Draw a parallelogram ABCD with diagonals AC and BD. State the given facts: ABCD is a parallelogram (so opposite sides are equal and parallel) and the diagonals are equal (&&AC = BD&&). - Step 2: Identify Triangles to Prove Congruent
To relate the interior angles, select two overlapping triangles that include the diagonals and share a common side. The best choice is &&\triangle ABC&& and &&\triangle DCB&&. - Step 3: Prove the Triangles Congruent using SSS Rule
Compare the sides of &&\triangle ABC&& and &&\triangle DCB&&. We have &&AB = DC&& (opposite sides of a parallelogram), &&BC = CB&& (common side), and &&AC = DB&& (given that diagonals are equal). Therefore, &&\triangle ABC \cong \triangle DCB&& by the SSS congruence rule. - Step 4: Use CPCTC to Find Equal Angles
Since the triangles are congruent, their corresponding angles are equal. By CPCTC (Corresponding Parts of Congruent Triangles are equal), we can conclude that &&\angle ABC = \angle DCB&&. - Step 5: Use Properties of Parallel Lines
Recall that in a parallelogram, adjacent sides are parallel (&&AB \parallel DC&&). With BC as a transversal, the sum of consecutive interior angles is &&180^\circ&&. Therefore, &&\angle ABC + \angle DCB = 180^\circ&&. - Step 6: Conclude the Proof
We know that &&\angle ABC = \angle DCB&& and their sum is &&180^\circ&&. This means each angle must be &&90^\circ&&. Since a parallelogram with one right angle is, by definition, a rectangle, we can conclude that ABCD is a rectangle.
Detailed Step-by-Step Proof 📝
Let ABCD be a parallelogram where the diagonals &&AC = BD&&.
Given: ABCD is a parallelogram and &&AC = BD&&.
To Prove: ABCD is a rectangle.
Proof:
To prove that ABCD is a rectangle, we need to show that one of its interior angles is &&90^\circ&&. Let’s consider the triangles &&\triangle ABC&& and &&\triangle DCB&&.
In &&\triangle ABC&& and &&\triangle DCB&&:
- &&AB = DC&& (Opposite sides of a parallelogram are equal) [S]
- &&BC = CB&& (Common side) [S]
- &&AC = DB&& (Given that the diagonals are equal) [S]
Therefore, by the SSS (Side-Side-Side) congruence rule, we have:
&&\triangle ABC \cong \triangle DCB&&
Since the two triangles are congruent, their corresponding parts must be equal (by CPCTC).
&&\implies \angle ABC = \angle DCB&& (by CPCTC)
Now, we know that in a parallelogram, opposite sides are parallel, so &&AB \parallel DC&&. Considering &&BC&& as the transversal, the sum of consecutive interior angles on the same side of the transversal is &&180^\circ&&.
&&\implies \angle ABC + \angle DCB = 180^\circ&&
Since &&\angle ABC = \angle DCB&&, we can substitute:
&&\implies \angle ABC + \angle ABC = 180^\circ&&
&&\implies 2\angle ABC = 180^\circ&&
&&\implies \angle ABC = \frac{180^\circ}{2} = 90^\circ&&
Conclusion:
Since ABCD is a parallelogram with one angle equal to &&90^\circ&&, it is a rectangle.
Hence, if the diagonals of a parallelogram are equal, then it is a rectangle.
Key Property of Rectangles ✅
This proof establishes a key property that distinguishes rectangles from other parallelograms: equal diagonals. While all parallelograms have diagonals that bisect each other, only rectangles (and squares) have diagonals that are equal in length.
FAQ (Frequently Asked Questions)
Q: What is the definition of a rectangle?
A: A rectangle is a parallelogram with at least one right angle (&&90^\circ&&). If one angle is &&90^\circ&&, it implies all four angles are &&90^\circ&&.
Q: What properties of a parallelogram are used in this proof?
A: Two key properties of a parallelogram are used: 1. Opposite sides are equal in length (&&AB = DC&&). 2. Opposite sides are parallel (&&AB \parallel DC&&), which leads to the property that consecutive interior angles sum to &&180^\circ&&.
Q: Why did we choose triangles ABC and DCB for the proof?
A: We chose these two triangles because they contain all the necessary parts: the two equal diagonals (&&AC&& and &&BD&&), the opposite sides of the parallelogram (&&AB&& and &&DC&&), and a common side (&&BC&&). This setup allows for a straightforward SSS congruence proof.
Q: What are consecutive interior angles?
A: When a transversal line intersects two parallel lines, the pair of angles that are on the same side of the transversal and between the two parallel lines are called consecutive interior angles. Their sum is always &&180^\circ&&. In this proof, &&BC&& is the transversal for parallel lines &&AB&& and &&DC&&.


