NCERT Solutions for Class 9 Maths Exercise 6.1 Question 3

Welcome, students! Here, we will break down the proof for Question 3 of Exercise 6.1 from the chapter on Lines and Angles. This solution uses a fundamental geometric rule, the Linear Pair Axiom, to arrive at the answer.
| Given Information | In &&\triangle PQR&& on the straight line SQT, we are given that &&\angle PQR = \angle PRQ&&. |
|---|---|
| To Prove | Prove that the exterior angles are equal: &&\angle PQS = \angle PRT&&. |
| Key Concept Used | Linear Pair Axiom: Angles on a straight line at a point add up to &&180^\circ&&. |
Question 3: In the figure, if &&\angle PQR = \angle PRQ&&, then prove that &&\angle PQS = \angle PRT&&.
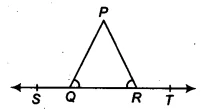
How to Prove &&\angle PQS = \angle PRT&& 🤔
This proof can be completed in four simple, logical steps. This method is also outlined in the `HowTo` schema to help search engines understand our solution.
- Step 1: Identify and Write Down the Linear Pair Equations
Recognize that SQT is a straight line. This creates two linear pairs. First, &&\angle PQS&& and &&\angle PQR&& form a linear pair, so &&\angle PQS + \angle PQR = 180^\circ&&. Second, &&\angle PRT&& and &&\angle PRQ&& form another linear pair, so &&\angle PRT + \angle PRQ = 180^\circ&&. - Step 2: Equate the Two Linear Pair Expressions
Since both expressions (&&\angle PQS + \angle PQR&&) and (&&\angle PRT + \angle PRQ&&) are equal to &&180^\circ&&, you can set them equal to each other. This gives the equation: &&\angle PQS + \angle PQR = \angle PRT + \angle PRQ&&. - Step 3: Use the Given Information to Substitute
The problem states that &&\angle PQR = \angle PRQ&&. Use this given equality to substitute one angle for the other in the equation from Step 2. For instance, replace &&\angle PRQ&& with &&\angle PQR&&. - Step 4: Simplify the Equation to Reach the Conclusion
After substitution, the equation becomes &&\angle PQS + \angle PQR = \angle PRT + \angle PQR&&. Now, you can cancel the common term &&\angle PQR&& from both sides. This leaves you with the final result: &&\angle PQS = \angle PRT&&. Hence, proved.
Detailed Step-by-Step Proof 📝
Let’s construct the proof using the information provided.
Given:
We are given that &&\angle PQR = \angle PRQ&&. … (Equation 1)
Using the Linear Pair Axiom:
From the figure, we can see that SQT is a straight line.
- At point Q, the ray QP stands on the line ST. Therefore, &&\angle PQS&& and &&\angle PQR&& form a linear pair.
&&\angle PQS + \angle PQR = 180^\circ&& … (Equation 2) - At point R, the ray RP stands on the line ST. Therefore, &&\angle PRT&& and &&\angle PRQ&& form a linear pair.
&&\angle PRT + \angle PRQ = 180^\circ&& … (Equation 3)
Combining the Equations:
From Equation 2 and Equation 3, since both are equal to &&180^\circ&&, we can set them equal to each other:
&&\angle PQS + \angle PQR = \angle PRT + \angle PRQ&&
Now, we use the information given in Equation 1 (&&\angle PQR = \angle PRQ&&). We can substitute &&\angle PRQ&& in our combined equation with &&\angle PQR&&:
&&\implies \angle PQS + \angle PQR = \angle PRT + \angle PQR&&
Conclusion:
By subtracting the common angle &&\angle PQR&& from both sides of the equation, we get:
&&\angle PQS = \angle PRT&&
Hence, proved.
Key Concept: Linear Pair Axiom ✅
This entire proof relies on the Linear Pair Axiom. It states that if a ray stands on a line, the sum of the two adjacent angles formed is &&180^\circ&&. Understanding this simple rule is crucial for solving many problems in the Lines and Angles chapter.
Common Mistakes to Avoid 🖍️
Some students might try to use the property that &&\triangle PQR&& is isosceles (since &&\angle PQR = \angle PRQ&&, it means sides &&PQ = PR&&). While this is true, it’s not needed for this proof and can overcomplicate the solution. The answer is found simply by analyzing the angles on the straight line.
FAQ (Frequently Asked Questions)
Q: What is the key concept used to solve this problem?
A: The key concept is the Linear Pair Axiom, which states that if a ray stands on a line, the sum of the two adjacent angles formed is &&180^\circ&&. We apply this axiom at both points Q and R on the straight line SQT.
Q: What does the given condition &&\angle PQR = \angle PRQ&& tell us about triangle PQR?
A: The condition &&\angle PQR = \angle PRQ&& means that the angles opposite to sides PR and PQ are equal. In a triangle, sides opposite to equal angles are also equal. Therefore, triangle PQR is an isosceles triangle with &&PQ = PR&&. However, this fact is not needed for this particular proof.
Q: Why can we set &&\angle PQS + \angle PQR&& equal to &&\angle PRT + \angle PRQ&&?
A: According to the linear pair axiom, both expressions equal &&180^\circ&&. Based on Euclid’s axiom that ‘things which are equal to the same thing are equal to one another,’ we can set the two expressions equal to each other.
Q: Are &&\angle PQS&& and &&\angle PRT&& exterior angles of the triangle?
A: Yes, &&\angle PQS&& and &&\angle PRT&& are the exterior angles of triangle PQR at vertices Q and R respectively. This problem essentially proves that if the interior opposite angles of a triangle are equal, then their corresponding exterior angles are also equal.
Further Reading
For more practice, refer to your official NCERT Class 9 Maths textbook, which you can find at https://ncert.nic.in/. Understanding axioms and theorems from this chapter is key to mastering geometry.


