NCERT Solutions for Class 9 Maths Exercise 6.1 Question 2

Hello students! This guide provides a detailed solution to Question 2 of Exercise 6.1 from the Lines and Angles chapter. This problem is a classic example of using the linear pair axiom and working with angles given as a ratio.
| Given Information | Lines &&XY&& and &&MN&& intersect at &&O&&, &&\angle POY = 90^\circ&&, and the ratio &&a : b = 2 : 3&&. |
|---|---|
| What to Find | The measure of angle &&c&&. |
| Final Answer | &&c = 126^\circ&& |
Question 2: In the figure, lines XY and MN intersect at O. If &&\angle POY = 90^\circ&& and &&a : b = 2 : 3&&, find c.
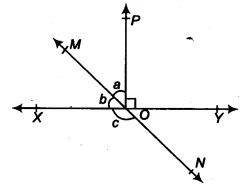
How to Find the Value of Angle c 🤔
Follow these four logical steps to arrive at the solution. This breakdown helps in understanding the flow of the proof.
- Step 1: Find the Sum of Angles ‘a’ and ‘b’
Recognize that &&XY&& is a straight line. The angles &&\angle XOM&&, &&\angle MOP&&, and &&\angle POY&& lie on this line, so their sum is &&180^\circ&&. Since &&\angle POY = 90^\circ&&, the sum of the remaining angles (&&a+b&&) must be &&180^\circ – 90^\circ = 90^\circ&&. - Step 2: Calculate the Individual Values of ‘a’ and ‘b’
We are given the ratio &&a : b = 2 : 3&&. Let &&a = 2x&& and &&b = 3x&&. Since &&a + b = 90^\circ&&, we can write &&2x + 3x = 90^\circ&&. This simplifies to &&5x = 90^\circ&&, which gives &&x = 18^\circ&&. Now find &&b&& by calculating &&3 \times 18^\circ&&, which is &&54^\circ&&. - Step 3: Use the Linear Pair Axiom on Line MN
Identify that &&MN&& is also a straight line. The angles &&b&& (&&\angle XOM&&) and &&c&& (&&\angle XON&&) are adjacent angles on this straight line, forming a linear pair. Therefore, their sum must be &&180^\circ&&. - Step 4: Calculate the Value of ‘c’
Set up the equation &&b + c = 180^\circ&&. Substitute the value of &&b&& (&&54^\circ&&) that you calculated in Step 2. This gives &&54^\circ + c = 180^\circ&&. Solving for &&c&&, we get &&c = 180^\circ – 54^\circ&&, which equals &&126^\circ&&.
Detailed Step-by-Step Solution 📝
Let’s start by analyzing the given information and the figure.
Step 1: Find the sum of a and b
Since &&XY&& is a straight line, the sum of angles on the line is &&180^\circ&&.
So, &&\angle XOM + \angle MOP + \angle POY = 180^\circ&&
From the figure, we know &&\angle XOM = b&&, &&\angle MOP = a&&, and we are given &&\angle POY = 90^\circ&&.
&&\implies b + a + 90^\circ = 180^\circ&&
&&\implies a + b = 180^\circ – 90^\circ&&
&&\implies a + b = 90^\circ&&
Step 2: Find the values of a and b using the ratio
We are given the ratio &&a : b = 2 : 3&&.
Let’s represent the angles with a common variable &&x&&. Let &&a = 2x&& and &&b = 3x&&.
Substituting these into our equation from Step 1:
&&2x + 3x = 90^\circ&&
&&5x = 90^\circ&&
&&x = \frac{90^\circ}{5} = 18^\circ&&
Now we can find the exact values of &&a&& and &&b&&:
- &&a = 2x = 2 \times 18^\circ = 36^\circ&&
- &&b = 3x = 3 \times 18^\circ = 54^\circ&&
Step 3: Find the value of c
Now, consider the straight line &&MN&&. The angles &&\angle XOM&& (which is &&b&&) and &&\angle XON&& (which is &&c&&) form a linear pair.
Therefore, their sum must be &&180^\circ&&.
&&b + c = 180^\circ&&
We substitute the value of &&b&& we found in Step 2:
&&54^\circ + c = 180^\circ&&
&&c = 180^\circ – 54^\circ&&
&&c = 126^\circ&&
Alternate Method (Trick) 💡
You can also find &&c&& using vertically opposite angles. Angle &&c&& is vertically opposite to &&\angle MOY&&. The angle &&\angle MOY = \angle MOP + \angle POY = a + 90^\circ&&. Since we found &&a = 36^\circ&&, then &&\angle MOY = 36^\circ + 90^\circ = 126^\circ&&. Because &&c = \angle MOY&&, we get &&c = 126^\circ&& directly!
Common Mistakes to Avoid 🖍️
A frequent error is to incorrectly set &&2x + 3x = 180^\circ&&. Remember that &&a&& and &&b&& together only make up a part of the straight line &&XY&&, specifically the part that is &&90^\circ&&. Always visualize which angles sum up to &&180^\circ&&.
FAQ (Frequently Asked Questions)
Q: How do you solve angles given in a ratio?
A: When angles are given in a ratio, like &&a : b = 2 : 3&&, you can represent them using a common variable ‘&&x&&’. So, &&a = 2x&& and &&b = 3x&&. Then you use other given information, like their sum (&&a + b = 90^\circ&&), to solve for &&x&& and find the individual angle measures.
Q: Why do angles b and c add up to 180°?
A: Angles &&b&& and &&c&& (which are &&\angle XOM&& and &&\angle XON&& respectively) lie on the straight line &&MN&&. Angles that are adjacent to each other on a straight line are called a linear pair, and their sum is always &&180^\circ&& according to the linear pair axiom.
Q: Is there an alternative method to find angle c?
A: Yes. Angle &&c&& is vertically opposite to &&\angle MOY&&. The angle &&\angle MOY&& is the sum of &&\angle MOP (a)&& and &&\angle POY (90^\circ)&&. After finding &&a = 36^\circ&&, you can calculate &&\angle MOY = 36^\circ + 90^\circ = 126^\circ&&. Since &&c&& is vertically opposite to &&\angle MOY&&, &&c&& must also be &&126^\circ&&.
Q: What are the individual values of angles a and b?
A: After finding that &&x = 18^\circ&&, the values of &&a&& and &&b&& are: &&a = 2x = 2 \times 18^\circ = 36^\circ&&, and &&b = 3x = 3 \times 18^\circ = 54^\circ&&.
Further Reading
For more practice with lines and angles, be sure to check out the other problems in your NCERT Class 9 Maths textbook, available at https://ncert.nic.in/.


