NCERT Solutions for Class 9 Maths Exercise 6.1 Question 5

Welcome, students! This guide from ncert solutions provides a detailed proof for Question 5 of Exercise 6.1. This is an excellent problem that combines basic geometry concepts with simple algebra to prove a relationship between angles.
| Given Information | POQ is a line, Ray OR is perpendicular to line PQ (&&OR \perp PQ&&), and OS is a ray between OP and OR. |
|---|---|
| To Prove | &&\angle ROS = \frac{1}{2} (\angle QOS – \angle POS)&& |
| Key Concept Used | Properties of perpendicular lines and linear pairs to set up algebraic equations. |
Question 5: In the figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that &&\angle ROS = \frac{1}{2} (\angle QOS – \angle POS)&&.
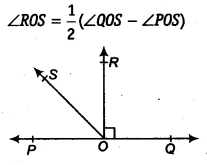
How to Prove the Angle Relationship 🤔
This proof can be achieved by following a clear, five-step algebraic approach.
- Step 1: Use the Perpendicular Property
Given that ray OR is perpendicular to the line PQ, we know that &&\angle ROQ = 90^\circ&&. Since POQ is a straight line, the adjacent angle &&\angle POR&& must also be &&90^\circ&& because &&180^\circ – 90^\circ = 90^\circ&&. - Step 2: Express &&\angle QOS&& Algebraically
From the figure, observe that the larger angle &&\angle QOS&& is the sum of two smaller angles, &&\angle ROQ&& and &&\angle ROS&&. Substitute the known value of &&\angle ROQ&& to get the expression: &&\angle QOS = 90^\circ + \angle ROS&&. - Step 3: Express &&\angle POS&& Algebraically
Similarly, observe that the &&90^\circ&& angle &&\angle POR&& is the sum of &&\angle POS&& and &&\angle ROS&&. This gives the equation &&90^\circ = \angle POS + \angle ROS&&. Rearrange this equation to express &&\angle POS&& in terms of &&\angle ROS&&: &&\angle POS = 90^\circ – \angle ROS&&. - Step 4: Substitute and Simplify the Expressions
Subtract the equation for &&\angle POS&& from the equation for &&\angle QOS&&. This gives: &&\angle QOS – \angle POS = (90^\circ + \angle ROS) – (90^\circ – \angle ROS)&&. Simplify the right-hand side to get &&\angle QOS – \angle POS = 2\angle ROS&&. - Step 5: Conclude the Proof
Rearrange the final equation to make &&\angle ROS&& the subject. This yields the required result: &&\angle ROS = \frac{1}{2} (\angle QOS – \angle POS)&&. Hence, proved.
Detailed Step-by-Step Proof 📝
Let’s use the given information to build our proof.
Given: POQ is a straight line and ray &&OR \perp PQ&&.
Since OR is perpendicular to PQ, we have:
&&\angle ROQ = 90^\circ&&
Also, since POQ is a straight line, the sum of angles on it is &&180^\circ&& (Linear Pair Axiom).
&&\angle POR + \angle ROQ = 180^\circ&&
&&\implies \angle POR + 90^\circ = 180^\circ&&
&&\implies \angle POR = 90^\circ&&
Now, we can express &&\angle POS&& and &&\angle QOS&& using the angles in the figure.
From the figure, we can see that &&\angle POR = \angle POS + \angle ROS&&.
&&\implies 90^\circ = \angle POS + \angle ROS&&
Let’s rearrange this to express &&\angle ROS&&:
&&\angle ROS = 90^\circ – \angle POS&& … (Equation 1)
Again, from the figure, we can see that &&\angle QOS = \angle ROQ + \angle ROS&&.
&&\implies \angle QOS = 90^\circ + \angle ROS&&
Let’s rearrange this to express &&\angle ROS&& again:
&&\angle ROS = \angle QOS – 90^\circ&& … (Equation 2)
Now, let’s add Equation 1 and Equation 2:
&&\angle ROS + \angle ROS = (90^\circ – \angle POS) + (\angle QOS – 90^\circ)&&
&&2\angle ROS = 90^\circ – \angle POS + \angle QOS – 90^\circ&&
The &&90^\circ&& terms cancel each other out:
&&2\angle ROS = \angle QOS – \angle POS&&
Finally, divide by 2 to get the required result:
&&\angle ROS = \frac{1}{2} (\angle QOS – \angle POS)&&
Hence, proved.
Key Strategy for Proofs ✅
A great strategy for proofs like this is to turn geometry into algebra. Express the angles you are working with (like &&\angle QOS&& and &&\angle POS&&) in terms of a common angle (&&\angle ROS&&). Once you have algebraic equations, you can add, subtract, or substitute them to arrive at the proof.
Common Mistakes to Avoid 🖍️
The most common mistake is getting confused about which angles add up to what. Carefully observe the figure. Notice that &&\angle POS&& and &&\angle ROS&& add up to the &&90^\circ&& angle &&\angle POR&&. In contrast, &&\angle ROQ&& and &&\angle ROS&& add up to the larger angle &&\angle QOS&&. Keeping this distinction clear is key.
FAQ (Frequently Asked Questions)
Q: What is the main strategy for this proof?
A: The main strategy is to treat the proof as an algebraic problem. We express the two key angles in the final expression (&&\angle QOS&& and &&\angle POS&&) in terms of the angle we want to find (&&\angle ROS&&) and the known &&90^\circ&& angle. Then, we manipulate these equations to arrive at the desired result.
Q: Why is &&\angle POR&& equal to &&90^\circ&&?
A: We are given that POQ is a straight line, which means the angles on it sum to &&180^\circ&&. We are also given that OR is perpendicular to PQ, which means &&\angle ROQ = 90^\circ&&. Therefore, its linear pair partner, &&\angle POR&&, must also be &&90^\circ&& because &&180^\circ – 90^\circ = 90^\circ&&.
Q: How is &&\angle QOS&& expressed in terms of &&\angle ROS&&?
A: From the figure, the angle &&\angle QOS&& is clearly the sum of &&\angle ROQ&& and &&\angle ROS&&. Since &&\angle ROQ = 90^\circ&&, the expression is &&\angle QOS = 90^\circ + \angle ROS&&.
Q: What is the key algebraic step in the proof?
A: One key method is to create two different expressions for &&\angle ROS&& and then add them together. This allows the other terms to be grouped and simplified, leading directly to the final proof.
Further Reading
For more practice with proofs involving lines and angles, consult your NCERT Class 9 Maths textbook. You can access it online at the official NCERT website: https://ncert.nic.in/.


