NCERT Solutions for Class 9 Maths Exercise 7.1 Question 1

Understanding the Question 🧐
In this problem, we are given a quadrilateral and some information about its sides and angles. Our goal is to use the rules of triangle congruence to prove that two triangles within the quadrilateral are identical in shape and size. After proving congruence, we need to comment on two of its other sides. This is a classic application of congruence rules, and these ncert solutions will guide you through every step.
In quadrilateral &&ACBD&&, &&AC = AD&& and &&AB&& bisects &&\angle A&&. Show that &&\triangle ABC \cong \triangle ABD&&. What can you say about &&BC&& and &&BD&&?
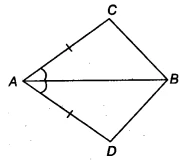
Step-by-Step Solution 📝
Let’s break down the proof into simple, logical steps.
Step 1: Identify the Given Information
First, we list what the question tells us. This is our starting point.
- We have a quadrilateral named &&ACBD&&.
- Side &&AC&& is equal to side &&AD&&. So, &&AC = AD&&.
- The line segment &&AB&& bisects &&\angle A&&. This means it cuts &&\angle A&& into two equal angles.
Step 2: Use the Angle Bisector Information
Since &&AB&& bisects &&\angle A&&, the two angles formed at vertex &&A&& are equal.
Therefore, &&\angle CAB = \angle DAB&&.
Step 3: Compare the Two Triangles
Now, let’s consider the two triangles we need to prove congruent: &&\triangle ABC&& and &&\triangle ABD&&. We will look for equal sides and angles.
- Side: &&AC = AD&& (This is given in the question)
- Angle: &&\angle CAB = \angle DAB&& (We found this in Step 2 because &&AB&& bisects &&\angle A&&)
- Side: &&AB = AB&& (This side is common to both triangles)
Step 4: Apply the Correct Congruence Rule
We have found two equal sides (&&AC&&, &&AB&&) and the angle included between them (&&\angle CAB&&) in &&\triangle ABC&&. These are equal to the corresponding two sides (&&AD&&, &&AB&&) and the included angle (&&\angle DAB&&) in &&\triangle ABD&&.
This matches the Side-Angle-Side (SAS) congruence criterion.
So, by the SAS congruence rule, we can state that:
&&\triangle ABC \cong \triangle ABD&&
Step 5: Determine the Relationship Between &&BC&& and &&BD&&
Now that we have proved the triangles are congruent, we can use the property of CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
This rule says that if two triangles are congruent, then all their corresponding parts (sides and angles) are also equal.
In our congruent triangles, &&\triangle ABC&& and &&\triangle ABD&&:
- The side corresponding to &&BC&& is &&BD&&.
Therefore, by CPCTC, we can conclude that &&BC = BD&&.
Conclusion and Key Points ✅
We have successfully shown that &&\triangle ABC \cong \triangle ABD&& using the SAS congruence rule. As a direct result of this congruence, we concluded that the lengths of the sides &&BC&& and &&BD&& are equal.
- SAS Congruence Rule: Two triangles are congruent if two sides and the included angle (the angle between those two sides) of one triangle are equal to the corresponding two sides and included angle of the other.
- CPCTC: This stands for “Corresponding Parts of Congruent Triangles are Congruent”. It is only used after you have proven that two triangles are congruent.
- An angle bisector is a line that divides an angle into two equal angles.
FAQ (Frequently Asked Questions)
Q: What is the SAS congruence rule?
A: The Side-Angle-Side (SAS) rule states that two triangles are congruent if two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of the other triangle. The angle must be between the two sides.
Q: Why is &&AB = AB&& in the proof?
A: The side &&AB&& is a common side for both triangles, &&\triangle ABC&& and &&\triangle ABD&&. Since it’s the exact same line segment for both triangles, its length is equal in both cases. This is often referred to as the “common side” or “reflexive property”.
Q: What does it mean for &&AB&& to bisect &&\angle A&&?
A: It means that the line segment &&AB&& divides &&\angle A&& into two equal angles. Therefore, &&\angle CAB = \angle DAB&&.
Q: What is CPCTC and when is it used?
A: CPCTC stands for ‘Corresponding Parts of Congruent Triangles are Congruent’. It is a theorem used only after you have proven that two triangles are congruent (e.g., by SAS, SSS, ASA, etc.). It allows you to state that the remaining corresponding sides and angles are also equal, as we did to show &&BC = BD&&.
Q: How do we prove &&\triangle ABC \cong \triangle ABD&&?
A: We use the SAS (Side-Angle-Side) congruence rule. We establish that &&AC = AD&& (Given Side), &&\angle CAB = \angle DAB&& (Given Angle), and &&AB = AB&& (Common Side). Since the angle is between the two sides, the triangles are congruent.
Q: What is the final conclusion about &&BC&& and &&BD&&?
A: The final conclusion is that &&BC = BD&&. This is determined by using CPCTC after proving that &&\triangle ABC \cong \triangle ABD&&.
Further Reading
For more information on triangle properties and congruence, you can refer to the official NCERT textbooks available on their website: https://ncert.nic.in/.


