NCERT Solutions for Class 9 Maths Exercise 7.2 Question 4

Welcome, students! This guide provides a detailed solution to Question 4 of Exercise 7.2 from the Triangles chapter. This problem is the converse of Question 3 and demonstrates how to prove a triangle is isosceles if its altitudes are equal, using the rules of congruence.
| Given Information | A triangle &&\triangle ABC&& with equal altitudes &&BE = CF&&. |
|---|---|
| To Prove | (i) &&\triangle ABE \cong \triangle ACF&& and (ii) &&AB = AC&& (i.e., &&\triangle ABC&& is isosceles). |
| Key Concept Used | AAS (Angle-Angle-Side) congruence rule. |
Question 4: ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Show that (i) &&\triangle ABE \cong \triangle ACF&& (ii) &&AB = AC&&, i.e., ABC is an isosceles triangle.
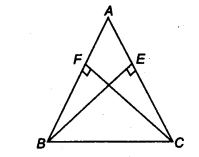
How to Prove &&\triangle ABE \cong \triangle ACF&& and &&AB = AC&& 🤔
This two-part proof can be completed in a few logical steps.
- Step 1: Identify Known Information in &&\triangle ABE&& and &&\triangle ACF&&
Start by considering the two triangles involved in the proof, &&\triangle ABE&& and &&\triangle ACF&&. List the equalities given in the problem:- &&\angle AEB = \angle AFC&& (both are &&90^\circ&& as BE and CF are altitudes).
- &&BE = CF&& (it’s given that the altitudes are equal).
- &&\angle A = \angle A&& (this angle is common to both triangles).
- Step 2: Apply the AAS Congruence Rule
With two corresponding angles (&&\angle A&& and the &&90^\circ&& angles) and a corresponding non-included side (&&BE&& and &&CF&&) being equal, we can apply the Angle-Angle-Side (AAS) congruence rule. This allows us to state that &&\triangle ABE \cong \triangle ACF&&. - Step 3: Use CPCTC to Prove &&AB = AC&&
Now that the triangles are proven congruent, we can use the principle of CPCTC (Corresponding Parts of Congruent Triangles are equal). The side corresponding to &&AB&& in &&\triangle ABE&& is &&AC&& in &&\triangle ACF&&. Therefore, we can conclude that &&AB = AC&&. - Step 4: Conclude that &&\triangle ABC&& is Isosceles
Since we have proved that two sides of &&\triangle ABC&& (&&AB&& and &&AC&&) are equal, by definition, &&\triangle ABC&& is an isosceles triangle. This completes the proof.
Detailed Step-by-Step Proof 📝
Here is the formal proof, broken down into the two parts required by the question.
Given:
In &&\triangle ABC&&, &&BE&& and &&CF&& are altitudes to the sides &&AC&& and &&AB&& respectively.
This means &&\angle AEB = 90^\circ&& and &&\angle AFC = 90^\circ&&.
We are also given that the altitudes are equal: &&BE = CF&&.
(i) Prove that &&\triangle ABE \cong \triangle ACF&&
Let’s consider the two triangles &&\triangle ABE&& and &&\triangle ACF&&.
In &&\triangle ABE&& and &&\triangle ACF&&:
- &&\angle A = \angle A&& (Common angle)
- &&\angle AEB = \angle AFC&& (Each &&90^\circ&&, since they are altitudes)
- &&BE = CF&& (Given)
Therefore, by the AAS (Angle-Angle-Side) congruence rule:
&&\triangle ABE \cong \triangle ACF&&
(ii) Prove that &&AB = AC&&, i.e., ABC is an isosceles triangle
Since we have already proved in part (i) that &&\triangle ABE \cong \triangle ACF&&, we can now use the property of congruent triangles.
By CPCTC (Corresponding Parts of Congruent Triangles are equal), the corresponding sides of these triangles must be equal.
The side corresponding to &&AB&& in &&\triangle ABE&& is &&AC&& in &&\triangle ACF&&.
So, &&AB = AC&&.
Conclusion:
Since two sides of &&\triangle ABC&& are equal, &&\triangle ABC&& is an isosceles triangle.
This is the Converse of Question 3! ✅
It’s helpful to notice that this problem is the exact opposite (or converse) of Question 3.
- In Q3: Given an isosceles triangle (AB=AC) &&\implies&& Prove altitudes are equal (BE=CF).
- In Q4: Given equal altitudes (BE=CF) &&\implies&& Prove the triangle is isosceles (AB=AC).
FAQ (Frequently Asked Questions)
Q: How is this question the converse of Question 3?
A: This question is the converse of Question 3 because the given information and the required proof are swapped. In Question 3, we were given an isosceles triangle (equal sides) and had to prove its altitudes were equal. In this question, we are given equal altitudes and must prove the triangle is isosceles (has equal sides).
Q: What is the AAS congruence rule?
A: The AAS (Angle-Angle-Side) congruence rule states that if two angles and a non-included side of one triangle are equal to the corresponding two angles and non-included side of another triangle, then the two triangles are congruent.
Q: Why is it important to use CPCTC?
A: CPCTC (Corresponding Parts of Congruent Triangles are equal) is the logical bridge that allows us to move from knowing that two triangles are congruent to knowing that their individual corresponding parts (sides and angles) are also equal. It’s the reason we provide to justify the conclusion &&AB = AC&& after proving &&\triangle ABE \cong \triangle ACF&&.
Q: What defines an isosceles triangle?
A: An isosceles triangle is defined as a triangle that has at least two sides of equal length. Proving that &&AB = AC&& fulfills this definition.


