NCERT Solutions for Class 9 Maths Exercise 7.2 Question 5

Welcome, students! This guide provides a clear and detailed proof for Question 5 of Exercise 7.2 from the chapter on Triangles. This problem is a fantastic application of the isosceles triangle theorem.
| Given Information | Two isosceles triangles, &&\triangle ABC&& (with &&AB = AC&&) and &&\triangle DBC&& (with &&DB = DC&&), are on the same base &&BC&&. |
|---|---|
| To Prove | &&\angle ABD = \angle ACD&&. |
| Key Concept Used | Isosceles Triangle Theorem: Angles opposite to equal sides of a triangle are equal. |
Question 5: ABC and DBC are two isosceles triangles on the same base BC. Show that &&\angle ABD = \angle ACD&&.
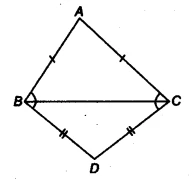
How to Prove &&\angle ABD = \angle ACD&& 🤔
This proof is quite straightforward and can be completed in four simple steps by looking at each triangle separately and then combining the results.
- Step 1: Analyze the First Isosceles Triangle (&&\triangle ABC&&)
Consider the larger isosceles triangle, &&\triangle ABC&&. Since it is given that &&AB = AC&&, we can apply the theorem that states angles opposite to equal sides are equal. This gives us &&\angle ABC = \angle ACB&&. Let’s call this Equation (1). - Step 2: Analyze the Second Isosceles Triangle (&&\triangle DBC&&)
Now, consider the smaller isosceles triangle, &&\triangle DBC&&. It is given that &&DB = DC&&. Applying the same theorem, we find that the angles opposite these sides are equal. This gives us &&\angle DBC = \angle DCB&&. Let’s call this Equation (2). - Step 3: Combine the Two Angle Equations
To find the complete angles &&\angle ABD&& and &&\angle ACD&&, we need to add the parts we found. Add Equation (1) and Equation (2). This results in &&(\angle ABC + \angle DBC) = (\angle ACB + \angle DCB)&&. - Step 4: Formulate the Conclusion
By observing the figure, we can see that the sum (&&\angle ABC + \angle DBC&&) is equal to the angle &&\angle ABD&&. Similarly, the sum (&&\angle ACB + \angle DCB&&) is equal to the angle &&\angle ACD&&. Therefore, by substituting these into our combined equation, we can conclude that &&\angle ABD = \angle ACD&&.
Detailed Step-by-Step Proof 📝
Here is the formal proof, written step-by-step.
Given:
&&\triangle ABC&& and &&\triangle DBC&& are two isosceles triangles on the same base &&BC&&.
In &&\triangle ABC&&, &&AB = AC&&.
In &&\triangle DBC&&, &&DB = DC&&.
To Prove:
We need to show that &&\angle ABD = \angle ACD&&.
Proof:
First, let’s consider &&\triangle ABC&&.
Since &&AB = AC&& (Given),
We know that angles opposite to equal sides of a triangle are equal.
Therefore, &&\angle ABC = \angle ACB&& … (Equation 1)
Next, let’s consider &&\triangle DBC&&.
Since &&DB = DC&& (Given),
The angles opposite to these sides must also be equal.
Therefore, &&\angle DBC = \angle DCB&& … (Equation 2)
Now, let’s add Equation 1 and Equation 2:
&&(\angle ABC) + (\angle DBC) = (\angle ACB) + (\angle DCB)&&
From the figure, it is clear that:
&&\angle ABC + \angle DBC = \angle ABD&&
&&\angle ACB + \angle DCB = \angle ACD&&
Substituting these into our combined equation, we get:
Conclusion:
&&\angle ABD = \angle ACD&&
Hence, proved.
Alternate Method (Using SSS Congruence) 💡
Another way to solve this is to draw a line segment joining A and D. Now, consider &&\triangle ABD&& and &&\triangle ACD&&.
- &&AB = AC&& (Given)
- &&DB = DC&& (Given)
- &&AD = AD&& (Common side)
FAQ (Frequently Asked Questions)
Q: What is the main theorem used in this proof?
A: The main theorem used is the Isosceles Triangle Theorem, which states that ‘angles opposite to equal sides of an isosceles triangle are equal.’ This theorem is applied to both triangle ABC and triangle DBC.
Q: Is there an alternative method to solve this problem?
A: Yes, there is an alternative method. You can draw a line segment connecting points A and D. Then, you can prove that triangle ABD is congruent to triangle ACD using the SSS (Side-Side-Side) congruence rule (since &&AB=AC&&, &&DB=DC&&, and &&AD&& is common). Once they are proven congruent, you can state that &&\angle ABD = \angle ACD&& by CPCTC.
Q: How is &&\angle ABD&& formed in the diagram?
A: The angle &&\angle ABD&& is formed by the sum of two smaller angles, &&\angle ABC&& and &&\angle DBC&&. Similarly, &&\angle ACD&& is formed by the sum of &&\angle ACB&& and &&\angle DCB&&.
Q: What does it mean for two triangles to be on the same base?
A: It means that both triangles share that side. In this problem, both &&\triangle ABC&& and &&\triangle DBC&& share the side &&BC&&. This is a common setup in geometry problems.


