NCERT Solutions for Class 9 Maths Exercise 7.3 Question 1

Welcome, students! This is a comprehensive guide to solving Question 1 of Exercise 7.3 from the chapter on Triangles. This is a multi-part proof that beautifully demonstrates how proving one result allows you to prove the next, using different triangle congruence rules.
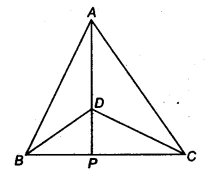
| Given Information | &&\triangle ABC&& and &&\triangle DBC&& are isosceles triangles on the same base &&BC&&, with &&AB = AC&& and &&DB = DC&&. |
|---|---|
| To Prove | (i) &&\triangle ABD \cong \triangle ACD&& (ii) &&\triangle ABP \cong \triangle ACP&& (iii) AP bisects &&\angle A&& and &&\angle D&& (iv) AP is the perpendicular bisector of &&BC&& |
| Key Concepts Used | SSS and SAS congruence rules, CPCTC, and Linear Pair Axiom. |
Question 1: &&\triangle ABC&& and &&\triangle DBC&& are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show the four results given above.
Detailed Step-by-Step Proof 📝
We will prove each of the four parts in sequence, as the result from each part helps in proving the next one.
(i) Prove that &&\triangle ABD \cong \triangle ACD&&
Let’s consider &&\triangle ABD&& and &&\triangle ACD&&.
- &&AB = AC&& (Given)
- &&DB = DC&& (Given)
- &&AD = AD&& (Common side)
Therefore, by the SSS (Side-Side-Side) congruence rule:
&&\triangle ABD \cong \triangle ACD&&
(ii) Prove that &&\triangle ABP \cong \triangle ACP&&
From part (i), we proved that &&\triangle ABD \cong \triangle ACD&&. By CPCTC (Corresponding Parts of Congruent Triangles are equal), we can say that &&\angle BAD = \angle CAD&&. This is the same as &&\angle BAP = \angle CAP&&.
Now, let’s consider &&\triangle ABP&& and &&\triangle ACP&&.
- &&AB = AC&& (Given)
- &&\angle BAP = \angle CAP&& (Proved above from part (i))
- &&AP = AP&& (Common side)
Therefore, by the SAS (Side-Angle-Side) congruence rule:
&&\triangle ABP \cong \triangle ACP&&
(iii) Prove that AP bisects &&\angle A&& as well as &&\angle D&&
AP bisects &&\angle A&&:
In part (i), we proved &&\triangle ABD \cong \triangle ACD&&. By CPCTC, this gives us &&\angle BAD = \angle CAD&&. Since P lies on the line AD, this means &&\angle BAP = \angle CAP&&. Therefore, AP bisects &&\angle A&&.
AP bisects &&\angle D&&:
To prove this, let’s consider &&\triangle DBP&& and &&\triangle DCP&&.
- &&DB = DC&& (Given)
- &&DP = DP&& (Common side)
- &&BP = CP&& (From part (ii), since &&\triangle ABP \cong \triangle ACP&&, by CPCTC)
Therefore, by the SSS congruence rule, &&\triangle DBP \cong \triangle DCP&&.
By CPCTC, this gives us &&\angle BDP = \angle CDP&&. This means that the line DP (which is an extension of AP) bisects &&\angle D&&.
Hence, AP bisects both &&\angle A&& and &&\angle D&&.
(iv) Prove that AP is the perpendicular bisector of BC
To be a perpendicular bisector, a line must do two things: bisect the segment and be perpendicular to it.
1. AP bisects BC:
From part (ii), we proved &&\triangle ABP \cong \triangle ACP&&. By CPCTC, we get &&BP = CP&&. This shows that P is the midpoint of BC, so AP bisects BC.
2. AP is perpendicular to BC:
Also from &&\triangle ABP \cong \triangle ACP&&, we get &&\angle APB = \angle APC&& by CPCTC.
Since &&\angle APB&& and &&\angle APC&& form a linear pair on the straight line BC, their sum is &&180^\circ&&.
&&\angle APB + \angle APC = 180^\circ&&
&&\implies \angle APB + \angle APB = 180^\circ&& (Since &&\angle APB = \angle APC&&)
&&\implies 2\angle APB = 180^\circ&&
&&\implies \angle APB = 90^\circ&&
This shows that AP is perpendicular to BC.
Since AP bisects BC and is perpendicular to it, AP is the perpendicular bisector of BC.
Building a Proof ✅
This question is a great example of a “chained proof.” Notice how the result from each part becomes a key piece of information for the next part.
- Part (i) gives us equal angles (by CPCTC).
- These angles are used in Part (ii) to prove a new congruence.
- The results of both Part (i) and Part (ii) are needed to prove Part (iii) and Part (iv).
FAQ (Frequently Asked Questions)
Q: What is the SSS congruence rule?
A: The SSS (Side-Side-Side) congruence rule states that if three sides of one triangle are equal to the three corresponding sides of another triangle, then the two triangles are congruent.
Q: What is the SAS congruence rule?
A: The SAS (Side-Angle-Side) congruence rule states that if two sides and the included angle (the angle between those two sides) of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.
Q: What is a perpendicular bisector?
A: A line is a perpendicular bisector of a segment if it cuts the segment into two equal parts (bisects it) and is also at a &&90&&-degree angle (perpendicular) to it.
Q: Why is this proof done in a specific order?
A: This proof is a chain of logical deductions. The result of each part is used to prove the next part. For example, proving the first congruence (&&\triangle ABD \cong \triangle ACD&&) gives us the equal angles needed to prove the second congruence (&&\triangle ABP \cong \triangle ACP&&), which in turn gives us the equal sides and angles needed to prove the final two parts.


