NCERT Solutions for Class 9 Maths Exercise 8.1 Question 3

Welcome, students! Let’s solve Question 3 from Exercise 8.1. This is a key proof that establishes a defining property of a rhombus. The proof uses the SAS congruence rule to show that if a quadrilateral’s diagonals are perpendicular bisectors of each other, it must have four equal sides.
| Given Information | A quadrilateral ABCD whose diagonals AC and BD bisect each other at right angles at point O. This means &&AO = OC, BO = OD,&& and &&\angle AOB = 90^\circ&&. |
|---|---|
| To Prove | ABCD is a rhombus (i.e., &&AB = BC = CD = DA&&). |
| Key Concept Used | SAS (Side-Angle-Side) congruence rule. |
Question 3: Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
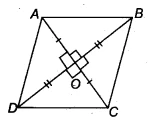
How to Prove the Quadrilateral is a Rhombus 🤔
This proof is a logical process of proving adjacent sides are equal, one pair at a time.
- Step 1: Draw and Label the Figure
Draw a quadrilateral ABCD with diagonals AC and BD intersecting at point O. Label the given information: the diagonals bisect each other (&&AO = OC&& and &&BO = OD&&) and they are perpendicular (all angles at O are &&90^\circ&&). - Step 2: Prove a Pair of Adjacent Sides are Equal
Select two adjacent triangles, such as &&\triangle AOD&& and &&\triangle COD&&. Use the SAS congruence rule to prove they are congruent: &&AO = CO&& (Given), &&\angle AOD = \angle COD&& (Both &&90^\circ&&), and &&DO = DO&& (Common). By CPCTC, this proves that the adjacent sides &&AD&& and &&CD&& are equal. - Step 3: Repeat the Process for Other Adjacent Sides
Similarly, prove that other pairs of adjacent triangles are congruent. For example, prove &&\triangle COD \cong \triangle COB&& using SAS to show that &&CD = CB&&. This establishes a chain of equal sides. - Step 4: Combine the Results to Show All Sides are Equal
By proving congruence for adjacent triangles around the center O, you can show that &&AD = CD, CD = CB,&& and &&CB = AB&&. Combining these results establishes that all four sides are equal: &&AB = BC = CD = DA&&. - Step 5: State the Final Conclusion
Since all four sides of the quadrilateral ABCD have been proven to be equal, it satisfies the definition of a rhombus. Therefore, ABCD is a rhombus.
Detailed Step-by-Step Proof 📝
Let ABCD be a quadrilateral where the diagonals AC and BD intersect at O.
Given:
The diagonals bisect each other at right angles. This means:
- &&AO = OC&& and &&BO = OD&&
- &&\angle AOB = \angle BOC = \angle COD = \angle DOA = 90^\circ&&
To Prove: ABCD is a rhombus.
Proof:
To prove that ABCD is a rhombus, we need to show that all four of its sides are equal (&&AB = BC = CD = DA&&). We can do this by proving the four small triangles formed by the diagonals are congruent to their adjacent triangles.
First, let’s consider &&\triangle AOD&& and &&\triangle COD&&.
In &&\triangle AOD&& and &&\triangle COD&&:
- &&AO = CO&& (Given, diagonals bisect each other) [S]
- &&\angle AOD = \angle COD&& (Each &&90^\circ&&, given) [A]
- &&OD = OD&& (Common side) [S]
Therefore, by the SAS congruence rule, &&\triangle AOD \cong \triangle COD&&.
By CPCTC (Corresponding Parts of Congruent Triangles are equal), we get:
&&AD = CD&& … (Equation 1)
Similarly, we can compare &&\triangle COD&& and &&\triangle COB&&:
- &&CO = CO&& (Common side)
- &&\angle COD = \angle COB&& (Each &&90^\circ&&)
- &&OD = OB&& (Given, diagonals bisect each other)
By the SAS congruence rule, &&\triangle COD \cong \triangle COB&&.
By CPCTC, we get:
&&CD = CB&& … (Equation 2)
Similarly, comparing &&\triangle COB&& and &&\triangle AOB&&, we can prove that &&CB = AB&&. … (Equation 3)
Conclusion:
From equations (1), (2), and (3), we have:
&&AD = CD = CB = AB&&
Since all four sides of the quadrilateral ABCD are equal, it is a rhombus by definition.
Hence, if the diagonals of a quadrilateral bisect each other at right angles, it is a rhombus.
Key Property of a Rhombus ✅
This proof establishes a key property that defines a rhombus: Its diagonals are perpendicular bisectors of each other. This is a two-way property:
- If a quadrilateral is a rhombus, its diagonals must be perpendicular bisectors.
- If a quadrilateral’s diagonals are perpendicular bisectors, it must be a rhombus (which is what we proved here).
FAQ (Frequently Asked Questions)
Q: What is the definition of a rhombus?
A: A rhombus is a quadrilateral in which all four sides are of equal length. Its diagonals also have the special property of being perpendicular bisectors of each other.
Q: What is the SAS congruence rule?
A: The SAS (Side-Angle-Side) congruence rule states that if two sides and the included angle (the angle between those two sides) of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.
Q: How do we know that all angles at the intersection point O are 90°?
A: The problem states that the diagonals bisect each other ‘at right angles’. This means they are perpendicular. If one angle at the intersection is &&90^\circ&&, the vertically opposite angle is also &&90^\circ&&, and the angles on a straight line (linear pair) must also sum to &&180^\circ&&, making all four angles at the intersection &&90^\circ&&.
Q: Is a square a rhombus?
A: Yes, a square is a special type of rhombus. A rhombus has all four sides equal. A square has all four sides equal and all four angles equal to &&90^\circ&&. So, every square is a rhombus, but not every rhombus is a square.


