NCERT Solutions for Class 9 Maths Exercise 8.1 Question 4

Welcome to the solution for Question 4 of Exercise 8.1. This is a fundamental proof where we will use the definition of a square to prove three important properties about its diagonals using different triangle congruence rules.
| Given Information | A square ABCD with diagonals AC and BD intersecting at O. |
|---|---|
| To Prove | (i) Diagonals are equal (&&AC = BD&&). (ii) Diagonals bisect each other (&&AO = OC, BO = OD&&). (iii) Diagonals bisect each other at right angles (&&\angle AOB = 90^\circ&&). |
| Key Concepts Used | Properties of a square, SAS, AAS, and SSS congruence rules, CPCTC. |
Question 4: Show that the diagonals of a square are equal and bisect each other at right angles.
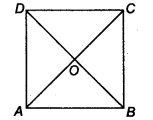
Detailed Step-by-Step Proof 📝
We will prove each of the three properties in sequence.
Given: ABCD is a square. This means all sides are equal (&&AB = BC = CD = DA&&), all angles are &&90^\circ&& (&&\angle A = \angle B = \angle C = \angle D = 90^\circ&&), and opposite sides are parallel (&&AB \parallel DC&& and &&AD \parallel BC&&).
(i) To Prove: The diagonals are equal (&&AC = BD&&)
Let’s consider the triangles &&\triangle ABC&& and &&\triangle DCB&&.
In &&\triangle ABC&& and &&\triangle DCB&&:
- &&AB = DC&& (Sides of a square are equal) [S]
- &&\angle ABC = \angle DCB&& (Each is &&90^\circ&&) [A]
- &&BC = CB&& (Common side) [S]
Therefore, by the SAS (Side-Angle-Side) congruence rule:
&&\triangle ABC \cong \triangle DCB&&
By CPCTC (Corresponding Parts of Congruent Triangles are equal), their corresponding parts are equal.
Hence, &&AC = BD&&.
(ii) To Prove: The diagonals bisect each other (&&AO = OC, BO = OD&&)
Let’s consider the triangles &&\triangle AOB&& and &&\triangle COD&&.
In &&\triangle AOB&& and &&\triangle COD&&:
- &&AB = CD&& (Sides of a square) [S]
- &&\angle OAB = \angle OCD&& (Alternate interior angles, since &&AB \parallel DC&&) [A]
- &&\angle OBA = \angle ODC&& (Alternate interior angles, since &&AB \parallel DC&&) [A]
Therefore, by the AAS (Angle-Angle-Side) congruence rule:
&&\triangle AOB \cong \triangle COD&&
By CPCTC, their corresponding parts are equal.
Hence, &&AO = OC&& and &&BO = OD&&.
(iii) To Prove: The diagonals bisect each other at right angles (&&\angle AOB = 90^\circ&&)
Let’s consider the adjacent triangles &&\triangle AOB&& and &&\triangle COB&&.
In &&\triangle AOB&& and &&\triangle COB&&:
- &&AB = CB&& (Sides of a square) [S]
- &&AO = CO&& (Proved in part (ii)) [S]
- &&BO = BO&& (Common side) [S]
Therefore, by the SSS (Side-Side-Side) congruence rule:
&&\triangle AOB \cong \triangle COB&&
By CPCTC, their corresponding angles are equal: &&\angle AOB = \angle COB&&.
We also know that &&\angle AOB&& and &&\angle COB&& form a linear pair on the straight line AC.
&&\implies \angle AOB + \angle COB = 180^\circ&&
Since &&\angle AOB = \angle COB&&, we can write:
&&\implies \angle AOB + \angle AOB = 180^\circ&&
&&\implies 2\angle AOB = 180^\circ \implies \angle AOB = 90^\circ&&
Hence, the diagonals bisect each other at right angles.
Summary of a Square’s Diagonal Properties ✅
This proof establishes the three essential properties of the diagonals of a square. A quadrilateral is a square if and only if its diagonals satisfy all three conditions:
- They are equal in length.
- They bisect each other.
- They are perpendicular to each other.
FAQ (Frequently Asked Questions)
Q: What is the definition of a square?
A: A square is a quadrilateral with four equal sides and four right angles (&&90^\circ&&). Because its opposite sides are equal and parallel, it is also a type of parallelogram, rhombus, and rectangle.
Q: What are alternate interior angles?
A: When a transversal line intersects two parallel lines, the pair of angles on opposite sides of the transversal and between the two parallel lines are called alternate interior angles. They are always equal. In this proof, we use this property because the opposite sides of a square are parallel.
Q: What is the difference between the diagonals of a square and a rhombus?
A: Both squares and rhombuses have diagonals that are perpendicular bisectors of each other. However, the diagonals of a square are always equal in length, while the diagonals of a non-square rhombus are not equal.
Q: What is the difference between the diagonals of a square and a rectangle?
A: Both squares and rectangles have diagonals that are equal in length and bisect each other. However, the diagonals of a square are always perpendicular to each other, while the diagonals of a non-square rectangle are not.


