NCERT Solutions for Class 9 Maths Exercise 8.1 Question 5

Welcome, students! Let’s solve Question 5 of Exercise 8.1. This is a comprehensive proof where we need to show that a quadrilateral is a square by using the properties of its diagonals. The strategy is to first prove it’s a rhombus, then prove it’s a rectangle, and combine the results.
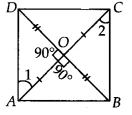
| Given Information | A quadrilateral ABCD where diagonals are equal (&&AC = BD&&) and are perpendicular bisectors of each other (&&AO = OC, BO = OD,&& and &&\angle AOB = 90^\circ&&). |
|---|---|
| To Prove | ABCD is a square. |
| Key Concepts Used | SAS and SSS congruence rules, CPCTC, and properties of parallelograms. |
Question 5: Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Detailed Step-by-Step Proof 📝
Let ABCD be a quadrilateral with diagonals AC and BD intersecting at O.
Given:
- Diagonals are equal: &&AC = BD&&
- Diagonals bisect each other: &&AO = OC&& and &&BO = OD&&
- Diagonals are perpendicular: &&\angle AOB = \angle BOC = \angle COD = \angle DOA = 90^\circ&&
To Prove: ABCD is a square.
The proof has two main parts:
Part 1: Prove that ABCD is a rhombus
To prove ABCD is a rhombus, we must show that all four sides are equal.
Let’s consider adjacent triangles &&\triangle AOD&& and &&\triangle COD&&.
- &&AO = CO&& (Given, diagonals bisect each other) [S]
- &&\angle AOD = \angle COD&& (Each &&90^\circ&&, given) [A]
- &&OD = OD&& (Common side) [S]
By the SAS congruence rule, &&\triangle AOD \cong \triangle COD&&.
By CPCTC, this gives us &&AD = CD&&. … (1)
Similarly, by proving &&\triangle COD \cong \triangle COB&&, we get &&CD = CB&&. … (2)
And by proving &&\triangle COB \cong \triangle AOB&&, we get &&CB = AB&&. … (3)
From (1), (2), and (3), we have &&AB = BC = CD = DA&&. Since all four sides are equal, ABCD is a rhombus.
Part 2: Prove that ABCD is a rectangle (has a right angle)
Now we prove that one of the interior angles of the rhombus is &&90^\circ&&. Let’s consider the overlapping triangles &&\triangle ABC&& and &&\triangle DCB&&.
- &&AB = DC&& (Sides of a rhombus, proved in Part 1) [S]
- &&BC = CB&& (Common side) [S]
- &&AC = BD&& (Given that diagonals are equal) [S]
By the SSS congruence rule, &&\triangle ABC \cong \triangle DCB&&.
By CPCTC, their corresponding angles are equal: &&\angle ABC = \angle DCB&&.
Since a rhombus is a parallelogram, its opposite sides are parallel (&&AB \parallel DC&&). With BC as the transversal, the sum of consecutive interior angles is &&180^\circ&&.
&&\implies \angle ABC + \angle DCB = 180^\circ&&
Since &&\angle ABC = \angle DCB&&, we can write &&2\angle ABC = 180^\circ&&, which gives &&\angle ABC = 90^\circ&&.
So, ABCD is a rhombus with one angle equal to &&90^\circ&&.
Conclusion
We have proved that ABCD is a rhombus (all sides are equal) and that it is also a rectangle (all angles are &&90^\circ&&).
A quadrilateral that is both a rhombus and a rectangle is defined as a square.
Therefore, ABCD is a square.
The Ultimate Quadrilateral ✅
This proof shows how a square inherits the properties of other quadrilaterals.
- Because its diagonals bisect each other, it’s a parallelogram.
- Because its diagonals are perpendicular, it’s a rhombus.
- Because its diagonals are equal, it’s a rectangle.
FAQ (Frequently Asked Questions)
Q: What is the definition of a square?
A: A square is a quadrilateral with four equal sides and four right angles (&&90^\circ&&). It is the only quadrilateral that is simultaneously a rhombus (equal sides) and a rectangle (equal angles).
Q: What three properties of diagonals guarantee a quadrilateral is a square?
A: A quadrilateral is a square if its diagonals are: 1. Equal in length. 2. Bisect each other. 3. Are perpendicular to each other.
Q: Why do we need to prove it’s a rhombus AND a rectangle?
A: Proving it’s a rhombus only shows that all sides are equal. Proving it’s a rectangle only shows that all angles are &&90^\circ&&. To satisfy the definition of a square, you must prove both conditions: all sides are equal AND all angles are &&90^\circ&&. The given properties of the diagonals allow us to prove both.
Q: How does this question relate to Questions 2, 3, and 4?
A: This question is a synthesis of the properties proved in the previous questions. Question 2 showed that a parallelogram with equal diagonals is a rectangle. Question 3 showed that a quadrilateral whose diagonals are perpendicular bisectors is a rhombus. This question gives you the conditions for both a rectangle and a rhombus, leading to the conclusion that it must be a square.


