NCERT Solutions for Class 9 Maths Exercise 6.1 Question 1

Welcome, students! Let’s solve the first question from the Lines and Angles chapter. This problem is a great warm-up, using two basic but very important concepts: vertically opposite angles and the linear pair axiom. This guide provides a clear, step-by-step solution.
| Given Information | Lines &&AB&& and &&CD&& intersect at &&O&&, &&\angle AOC + \angle BOE = 70^\circ&&, and &&\angle BOD = 40^\circ&&. |
|---|---|
| What to Find | The measure of &&\angle BOE&& and reflex &&\angle COE&&. |
| Final Answer | &&\angle BOE = 30^\circ&& and reflex &&\angle COE = 250^\circ&&. |
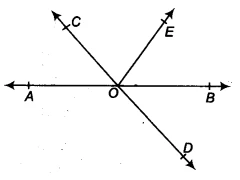
Question 1: In the figure, lines AB and CD intersect at O. If &&\angle AOC + \angle BOE = 70^\circ&& and &&\angle BOD = 40^\circ&&, find &&\angle BOE&& and reflex &&\angle COE&&.
How to Find &&\angle BOE&& and reflex &&\angle COE&& 🤔
Follow these logical steps to solve the problem. The text here exactly matches the `HowTo` schema to help search engines understand our method.
- Step 1: Use Vertically Opposite Angles to find &&\angle AOC&&
Identify that lines &&AB&& and &&CD&& intersect at &&O&&. This means that &&\angle AOC&& and &&\angle BOD&& are vertically opposite angles. Since vertically opposite angles are equal and &&\angle BOD = 40^\circ&&, it follows that &&\angle AOC = 40^\circ&&. - Step 2: Use the Given Sum to Find &&\angle BOE&&
The problem states that &&\angle AOC + \angle BOE = 70^\circ&&. Substitute the value of &&\angle AOC&& found in the previous step (&&40^\circ&&) into this equation. This gives &&40^\circ + \angle BOE = 70^\circ&&. Solving for &&\angle BOE&&, we get &&\angle BOE = 30^\circ&&. - Step 3: Use Linear Pair of Angles to Find &&\angle COE&&
Recognize that &&AOB&& is a straight line. The sum of all angles on a straight line is &&180^\circ&&. Therefore, &&\angle AOC + \angle COE + \angle BOE = 180^\circ&&. Since we know &&(\angle AOC + \angle BOE) = 70^\circ&&, we can write &&70^\circ + \angle COE = 180^\circ&&. Solving for &&\angle COE&&, we get &&\angle COE = 110^\circ&&. - Step 4: Calculate the Reflex Angle for &&\angle COE&&
A reflex angle is the angle that is greater than &&180^\circ&& and less than &&360^\circ&&. To find the reflex &&\angle COE&&, subtract the value of &&\angle COE&& from &&360^\circ&&. This gives Reflex &&\angle COE = 360^\circ – 110^\circ = 250^\circ&&.
Detailed Step-by-Step Solution 📝
Let’s solve this problem by finding each required angle one by one.
Part 1: Finding the value of &&\angle BOE&&
We are given that lines &&AB&& and &&CD&& intersect at point &&O&&.
When two lines intersect, the vertically opposite angles formed are equal.
Therefore, &&\angle AOC = \angle BOD&&.
It is given that &&\angle BOD = 40^\circ&&. So, &&\angle AOC = 40^\circ&&.
We are also given the sum: &&\angle AOC + \angle BOE = 70^\circ&&.
Now, we substitute the value of &&\angle AOC&& into this equation:
&&\implies 40^\circ + \angle BOE = 70^\circ&&
&&\implies \angle BOE = 70^\circ – 40^\circ&&
&&\angle BOE = 30^\circ&&
Part 2: Finding the value of reflex &&\angle COE&&
To find the reflex &&\angle COE&&, we first need to find the regular &&\angle COE&&.
Since &&AOB&& is a straight line, the sum of all angles on it is &&180^\circ&& (Linear Pair Axiom).
From the figure, we can write:
&&\angle AOC + \angle COE + \angle BOE = 180^\circ&&
We can group the first and last terms because we know their sum:
&&(\angle AOC + \angle BOE) + \angle COE = 180^\circ&&
Substitute the given value &&\angle AOC + \angle BOE = 70^\circ&&:
&&\implies 70^\circ + \angle COE = 180^\circ&&
&&\implies \angle COE = 180^\circ – 70^\circ&&
&&\implies \angle COE = 110^\circ&&
Now, we can find the reflex angle. A reflex angle is &&360^\circ&& minus the angle.
Reflex &&\angle COE = 360^\circ – \angle COE&&
&&\implies \text{Reflex } \angle COE = 360^\circ – 110^\circ&&
Reflex &&\angle COE = 250^\circ&&
Common Mistakes to Avoid 🖍️
A common mistake is to stop after finding &&\angle COE = 110^\circ&&. The question specifically asks for the reflex &&\angle COE&&. Always double-check what the question is asking for to ensure you don’t miss the final step!
Key Concepts Used ✅
- Vertically Opposite Angles: When two lines intersect, the angles opposite each other are equal.
- Linear Pair Axiom: The sum of angles on a straight line is always &&180^\circ&&.
- Reflex Angle: An angle greater than &&180^\circ&& but less than &&360^\circ&&. It’s calculated as &&360^\circ – \text{angle}&&.
FAQ (Frequently Asked Questions)
Q: What are vertically opposite angles?
A: Vertically opposite angles are the angles opposite each other when two lines intersect. They are always equal. In this problem, &&\angle AOC&& and &&\angle BOD&& are vertically opposite angles.
Q: What is a linear pair of angles?
A: A linear pair of angles are two adjacent angles formed by intersecting lines whose non-common sides are opposite rays. The sum of the angles in a linear pair is always &&180^\circ&&. The concept extends to all angles on a straight line, which must also sum to &&180^\circ&&.
Q: How do you calculate a reflex angle?
A: To find the reflex of an angle, you subtract the angle’s measure from &&360^\circ&&. For example, the reflex of a &&110^\circ&& angle is &&360^\circ – 110^\circ = 250^\circ&&.
Q: What is the value of &&\angle COE&& in this question?
A: The value of &&\angle COE&& is &&110^\circ&&. It is found by using the linear pair axiom on the straight line &&AB&&, where &&\angle AOC + \angle COE + \angle BOE = 180^\circ&&. Substituting the given sum &&\angle AOC + \angle BOE = 70^\circ&&, we get &&70^\circ + \angle COE = 180^\circ&&, which gives &&\angle COE = 110^\circ&&.
Further Reading
For more examples and a deeper dive into the properties of lines and angles, refer to your official NCERT Class 9 Maths textbook, which you can find at https://ncert.nic.in/.


