NCERT Solutions for Class 9 Maths Exercise 6.2 Question 1

Understanding the Question 🧐
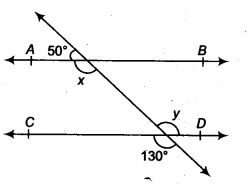
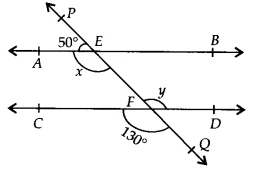
In this problem, we’re given a figure with two lines, &&AB&& and &&CD&&, intersected by a third line called a transversal. Our goals are twofold: first, to find the values of the unknown angles &&x&& and &&y&&, and second, to use these values to prove that the lines &&AB&& and &&CD&& are parallel to each other. This is a fundamental problem in geometry that uses basic angle properties. We will be using the concepts of linear pairs and vertically opposite angles to solve this. These ncert solutions will guide you through each step.
In the given figure, find the values of &&x&& and &&y&& and then show that &&AB \parallel CD&&.
Step-by-Step Solution 📝
Part 1: Finding the value of &&x&&
Let’s look at the top intersection point on the transversal line. The angle marked &&50°&& and the angle &&x&& are next to each other on a straight line. This means they form a linear pair.
The Linear Pair Axiom states that the sum of angles in a linear pair is always &&180°&&.
So, we can write the equation:
&&50° + x = 180°&&
To find &&x&&, we subtract &&50°&& from both sides:
&&x = 180° – 50°&&
This gives us the value of &&x&&:
&&x = 130°&&
Part 2: Finding the value of &&y&&
Now, let’s look at the bottom intersection point. The angle &&y&& and the angle marked &&130°&& are opposite to each other where the two lines cross. These are called vertically opposite angles.
A key property in geometry is that vertically opposite angles are always equal.
Therefore, we can directly state the value of &&y&&:
&&y = 130°&&
Part 3: Proving that &&AB \parallel CD&&
We have now found the values of both angles: &&x = 130°&& and &&y = 130°&&.
From our calculations, we can see that &&x = y&&.
If we observe the positions of angle &&x&& and angle &&y&& relative to the lines &&AB&& and &&CD&& and the transversal, we can see they are a pair of alternate interior angles.
The Converse of the Alternate Interior Angles Theorem states that if a transversal intersects two lines such that the alternate interior angles are equal, then the two lines are parallel.
Since we have shown that &&x = y = 130°&&, the condition for this theorem is met.
Thus, we can conclude that &&AB \parallel CD&&.
Conclusion and Key Points ✅
We have successfully solved the problem by first finding the values of the angles and then using those values to prove the lines are parallel.
The final results are:
- The value of angle &&x&& is &&130°&&.
- The value of angle &&y&& is &&130°&&.
- Since the alternate interior angles (&&x&& and &&y&&) are equal, the lines &&AB&& and &&CD&& are parallel (&&AB \parallel CD&&).
- Angles on a straight line that are adjacent (a linear pair) always sum to &&180°&&.
- Angles formed by intersecting lines that are opposite to each other (vertically opposite) are always equal.
- If a pair of alternate interior angles are equal, then the lines cut by the transversal are parallel. This is a crucial condition for proving lines are parallel.
FAQ ❓
Q: What is a linear pair of angles?
A: A linear pair of angles consists of two adjacent angles whose non-common sides form a straight line. The sum of the angles in a linear pair is always &&180°&&.
Q: How do you find the value of &&x&& in this question?
A: The angle &&x&& and the &&50°&& angle are on a straight line, forming a linear pair. So, their sum is &&180°&&. The equation is &&x + 50° = 180°&&, which gives &&x = 130°&&.
Q: What are vertically opposite angles?
A: When two lines intersect, they form two pairs of opposite angles. These pairs are called vertically opposite angles. They are always equal to each other.
Q: How is the value of &&y&& determined in the solution?
A: Angle &&y&& is vertically opposite to the &&130°&& angle shown in the figure. Because vertically opposite angles are equal, we can conclude that &&y = 130°&&.
Q: What condition proves that line &&AB&& is parallel to line &&CD&&?
A: We prove that &&AB \parallel CD&& by using the converse of the Alternate Interior Angles Theorem. After calculating &&x = 130°&& and &&y = 130°&&, we see that the alternate interior angles &&x&& and &&y&& are equal. This equality is the condition that proves the lines are parallel.
Further Reading 📚
For more information on lines and angles, you can refer to the official NCERT textbook for Class 9 Maths. You can find the textbooks and other resources on the official NCERT website: https://ncert.nic.in/.


