NCERT Solutions for Class 9 Maths Exercise 6.2 Question 5

Understanding the Question 🧐
This problem tests our understanding of angles formed by transversals intersecting parallel lines. We are given a figure with two parallel lines and are asked to find the values of two unknown angles, labeled &&x&& and &&y&&. By applying the correct geometric theorems, we can easily solve for these values. Let’s break down these ncert solutions step by step.
In the given figure, if &&AB || CD&&, &&∠APQ = 50^\circ&&, and &&∠PRD = 127^\circ&&, find &&x&& and &&y&&.
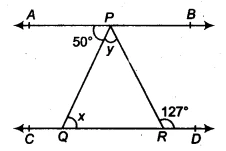
Given Information:
- Line &&AB&& is parallel to line &&CD&& (i.e., &&AB || CD&&).
- &&\angle APQ = 50^\circ&&.
- &&\angle PRD = 127^\circ&&.
To Find:
- The value of &&x&& (which represents &&\angle PQR&&).
- The value of &&y&& (which represents &&\angle QPR&&).
Part 1: Finding the value of &&x&& 📝
Step 1: Identify the relationship between the angles.
We have parallel lines &&AB&& and &&CD&&, and the line &&PQ&& acts as a transversal.
The angles &&\angle APQ&& and &&\angle PQR&& (which is &&x&&) are a pair of alternate interior angles.
Step 2: Apply the Alternate Interior Angles Theorem.
This theorem states that when a transversal intersects two parallel lines, the alternate interior angles are equal.
Therefore, &&\angle PQR = \angle APQ&&.
Step 3: Substitute the given value.
We are given that &&\angle APQ = 50^\circ&&.
So, &&x = 50^\circ&&.
Part 2: Finding the value of &&y&& 📝
Step 1: Identify the relevant transversal and angles.
Now, let’s consider &&PR&& as the transversal intersecting the parallel lines &&AB&& and &&CD&&.
The entire angle &&\angle APR&& and the angle &&\angle PRD&& are a pair of alternate interior angles.
Step 2: Apply the Alternate Interior Angles Theorem again.
According to the theorem, &&\angle APR = \angle PRD&&.
Step 3: Express &&\angle APR&& in terms of known angles and &&y&&.
From the figure, we can see that the angle &&\angle APR&& is made up of two adjacent angles: &&\angle APQ&& and &&\angle QPR&& (which is &&y&&).
So, &&\angle APR = \angle APQ + \angle QPR&&.
Substituting the variables and known values, we get: &&\angle APR = 50^\circ + y&&.
Step 4: Set up the equation and solve for &&y&&.
From Step 2, we know &&\angle APR = \angle PRD&&. Let’s substitute the expressions for these angles:
&&50^\circ + y = \angle PRD&&
We are given &&\angle PRD = 127^\circ&&.
&&50^\circ + y = 127^\circ&&
To find &&y&&, subtract &&50^\circ&& from &&127^\circ&&.
&&y = 127^\circ – 50^\circ&&
&&y = 77^\circ&&.
Conclusion and Key Points ✅
By applying the alternate interior angles theorem twice with two different transversals, we have found the values of both unknown angles.
The final answers are:
- &&x = 50^\circ&&
- &&y = 77^\circ&&
- When a transversal intersects two parallel lines, alternate interior angles are equal.
- A larger angle can be expressed as the sum of its smaller adjacent angles.
- (Alternative Method) The sum of all angles in a triangle is always &&180^\circ&&. You can use this property to verify your answer for &&y&&.
Frequently Asked Questions (FAQ)
Q: How do you find the value of &&x&& in this problem?
A: The value of &&x&& is found by recognizing that angle &&x&& (&&\angle PQR&&) and the given &&50^\circ&& angle (&&\angle APQ&&) are alternate interior angles. They are formed by the transversal &&PQ&& intersecting the parallel lines &&AB&& and &&CD&&. Since alternate interior angles are equal, &&x = 50^\circ&&.
Q: What theorem is used to find the value of &&y&&?
A: To find &&y&&, we use the alternate interior angles theorem again. This time, we consider &&PR&& as the transversal. The entire angle &&\angle APR&& (which is the sum of &&50^\circ&& and &&y&&) is equal to the given angle &&\angle PRD&& (&&127^\circ&&). This allows us to set up the equation &&50^\circ + y = 127^\circ&& and solve for &&y&&.
Q: Is there an alternative method to find &&y&&?
A: Yes. After finding &&x = 50^\circ&&, you can find &&\angle PRQ&&. Since &&\angle PRQ&& and &&\angle PRD&& form a linear pair on the line &&CD&&, &&\angle PRQ = 180^\circ – 127^\circ = 53^\circ&&. Then, using the angle sum property in triangle &&PQR&& (&&x + y + \angle PRQ = 180^\circ&&), you can substitute the known values: &&50^\circ + y + 53^\circ = 180^\circ&&. Solving this gives &&y = 77^\circ&&.
Q: What are alternate interior angles?
A: Alternate interior angles are a pair of angles on opposite sides of a transversal line and are located in the ‘interior’ region between the two parallel lines. A fundamental theorem in geometry states that these angles are always equal.
Q: Why is the entire angle &&\angle APR&& equal to &&127^\circ&&?
A: The entire angle &&\angle APR&& is equal to &&\angle PRD&& (which is &&127^\circ&&) because they are a pair of alternate interior angles. This relationship exists because the line segment &&PR&& acts as a transversal intersecting the two parallel lines &&AB&& and &&CD&&.
Further Reading
For more details on the properties of lines and angles, you can refer to the official NCERT textbook provided by the National Council of Educational Research and Training. Visit their website at https://ncert.nic.in/ for official resources.


