NCERT Solutions for Class 9 Maths Exercise 6.2 Question 6

Understanding the Question 🧐
This is a fascinating problem that combines a concept from Physics (the Law of Reflection) with our knowledge of Geometry. We are given two parallel mirrors and a light ray that reflects off both. Our goal is to prove that the initial path of the light ray is parallel to its final path. This ncert solutions will guide you through the formal proof.
In the given figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C, and again reflects back along CD. Prove that &&AB || CD&&.
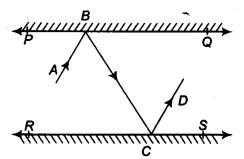
Given:
- Two parallel mirrors, &&PQ || RS&&.
- A light ray reflects from B on mirror PQ to C on mirror RS, and then reflects along CD.
To Prove:
- The incident ray &&AB&& is parallel to the final reflected ray &&CD&& (i.e., &&AB || CD&&).
Proof: Step-by-Step Solution 📝
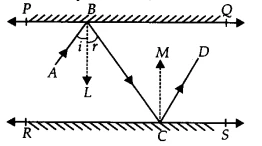
Step 1: Construction 🏗️
To apply the Law of Reflection, we need to draw normals (lines perpendicular to the mirrors) at the points of reflection.
- Draw a normal &&BM&& to the mirror &&PQ&& at point B (so, &&BM \perp PQ&&).
- Draw a normal &&CN&& to the mirror &&RS&& at point C (so, &&CN \perp RS&&).
Step 2: Applying the Law of Reflection
The Law of Reflection states that the angle of incidence is equal to the angle of reflection.
At mirror PQ (point B):
- Angle of incidence = &&\angle ABM&&. Let’s call this &&\angle 1&&.
- Angle of reflection = &&\angle MBC&&. Let’s call this &&\angle 2&&.
- By the Law of Reflection: &&\angle 1 = \angle 2&& …(i)
At mirror RS (point C):
- Angle of incidence = &&\angle BCN&&. Let’s call this &&\angle 3&&.
- Angle of reflection = &&\angle NCD&&. Let’s call this &&\angle 4&&.
- By the Law of Reflection: &&\angle 3 = \angle 4&& …(ii)
Step 3: Relating the Normals and Angles
We know that the mirrors are parallel (&&PQ || RS&&). Since &&BM&& and &&CN&& are normals (perpendicular) to these parallel lines, the normals themselves must be parallel.
So, &&BM || CN&&.
Now, consider &&BM || CN&& with the line &&BC&& as the transversal. The angles &&\angle 2&& and &&\angle 3&& are alternate interior angles.
Since the lines are parallel, these angles must be equal.
Therefore, &&\angle 2 = \angle 3&& …(iii)
Step 4: Combining the Results and Final Proof
From our three equations, we have:
- &&\angle 1 = \angle 2&& (from i)
- &&\angle 3 = \angle 4&& (from ii)
- &&\angle 2 = \angle 3&& (from iii)
Combining these, we can conclude that all four angles are equal: &&\angle 1 = \angle 2 = \angle 3 = \angle 4&&.
Now let’s look at the larger angles, &&\angle ABC&& and &&\angle DCB&&:
&&\angle ABC = \angle 1 + \angle 2 = \angle 2 + \angle 2 = 2\angle 2&&
&&\angle DCB = \angle 3 + \angle 4 = \angle 3 + \angle 3 = 2\angle 3&&
Since &&\angle 2 = \angle 3&&, it follows that &&2\angle 2 = 2\angle 3&&.
This means &&\angle ABC = \angle DCB&&.
These two equal angles, &&\angle ABC&& and &&\angle DCB&&, are a pair of alternate interior angles for the lines &&AB&& and &&CD&& with transversal &&BC&&. According to the Converse of the Alternate Interior Angles Theorem, if the alternate interior angles are equal, the lines must be parallel.
Hence, &&AB || CD&&.
(Proved)
Conclusion and Key Points ✅
We have successfully proven that the incident ray &&AB&& is parallel to the reflected ray &&CD&&. This elegant proof combines a fundamental principle of physics with key geometric theorems about parallel lines.
- Law of Reflection: The angle of incidence is equal to the angle of reflection (&&\angle i = \angle r&&).
- Normals drawn to a pair of parallel lines are themselves parallel.
- Converse of Alternate Interior Angles Theorem: If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
Frequently Asked Questions (FAQ)
Q: What is the Law of Reflection?
A: The Law of Reflection is a principle in optics that states the angle of incidence (the angle between the incoming ray and the normal) is equal to the angle of reflection (the angle between the reflected ray and the normal).
Q: Why is it necessary to draw normals in this proof?
A: The Law of Reflection is defined with respect to the normal (a line perpendicular to the mirror’s surface). To apply this law to the light rays &&AB&& and &&CD&&, we must first construct normals at the points of reflection (&&B&& and &&C&&). These normals give us the angles of incidence and reflection needed for the proof.
Q: Why are the constructed normals BM and CN parallel?
A: The normals are drawn perpendicular to the mirrors &&PQ&& and &&RS&&, respectively. Since the mirrors &&PQ&& and &&RS&& are given as parallel, any lines that are perpendicular to them must also be parallel to each other. Therefore, &&BM || CN&&.
Q: How did we prove ∠ABC is equal to ∠DCB?
A: We first used the Law of Reflection to show that the smaller angles around the normals are equal (&&\angle 1 = \angle 2&& and &&\angle 3 = \angle 4&&). Then, by proving the normals are parallel, we showed that the alternate interior angles &&\angle 2&& and &&\angle 3&& are equal. This implies all four small angles are equal. Since &&\angle ABC = \angle 1 + \angle 2&& and &&\angle DCB = \angle 3 + \angle 4&&, their sums must be equal.
Q: What is the final geometric theorem used to prove AB || CD?
A: The final step uses the Converse of the Alternate Interior Angles Theorem. After we prove that the alternate interior angles &&\angle ABC&& and &&\angle DCB&& are equal, this theorem allows us to conclude that the lines &&AB&& and &&CD&& must be parallel.
Further Reading
For more details on the properties of lines and angles, you can refer to the official NCERT textbook provided by the National Council of Educational Research and Training. Visit their website at https://ncert.nic.in/ for official resources.


