NCERT Solutions for Class 9 Maths Exercise 7.1 Question 4

Understanding the Question 🧐
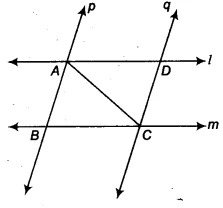
In this problem, we are given a geometric figure created by two pairs of parallel lines that intersect each other. This setup forms a parallelogram which is divided into two triangles by a diagonal. Our goal is to prove that these two triangles are congruent. This question is a great exercise in using the properties of parallel lines to solve congruence problems. These ncert solutions will walk you through the proof step-by-step.
&&l&& and &&m&& are two parallel lines intersected by another pair of parallel lines &&p&& and &&q&&. Show that &&\triangle ABC \cong \triangle CDA&&.
Step-by-Step Solution 📝
Step 1: Identify the Given Information and Analyze the Figure
From the question and the figure, we know:
- Line &&l&& is parallel to line &&m&& (i.e., &&l \parallel m&&). Since the line segments &&AD&& and &&BC&& lie on &&l&& and &&m&& respectively, we have &&AD \parallel BC&&.
- Line &&p&& is parallel to line &&q&& (i.e., &&p \parallel q&&). Since the line segments &&AB&& and &&DC&& lie on &&p&& and &&q&& respectively, we have &&AB \parallel DC&&.
- The quadrilateral formed is &&ABCD&&, and &&AC&& is a diagonal.
Step 2: Use Properties of Parallel Lines and Transversals
We can use the diagonal &&AC&& as a transversal for both pairs of parallel lines to find equal angles.
- Consider &&p \parallel q&& with transversal &&AC&&. The alternate interior angles are equal.
Therefore, &&\angle BAC = \angle DCA&& — (1) - Consider &&l \parallel m&& with transversal &&AC&&. The alternate interior angles are equal.
Therefore, &&\angle BCA = \angle DAC&& — (2)
Step 3: Compare the Two Triangles (&&\triangle ABC&& and &&\triangle CDA&&)
Now let’s list the equal parts we have found for the two triangles:
- Angle: &&\angle BAC = \angle DCA&& (From equation (1))
- Side: &&AC = CA&& (This is the common side to both triangles)
- Angle: &&\angle BCA = \angle DAC&& (From equation (2))
Step 4: Apply the Correct Congruence Rule
We have two angles and the side that is included between them. This combination perfectly matches the Angle-Side-Angle (ASA) congruence criterion.
So, by the ASA congruence rule, we can state that:
&&\triangle ABC \cong \triangle CDA&&
(Hence Proved)
Conclusion and Key Points ✅
We have successfully proven that &&\triangle ABC \cong \triangle CDA&&. The proof was built upon the fundamental property that when a transversal intersects parallel lines, the alternate interior angles are equal. By identifying two such pairs of angles and the common side between them, we applied the ASA congruence rule to reach our conclusion. This also demonstrates a key property of parallelograms: a diagonal divides it into two congruent triangles.
- ASA Congruence Rule: Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and included side of the other triangle.
- Alternate Interior Angles: When a transversal intersects two parallel lines, the angles that are on opposite sides of the transversal and inside the parallel lines are equal.
- A quadrilateral with two pairs of parallel opposite sides is a parallelogram.
FAQ (Frequently Asked Questions)
Q: What is the ASA congruence rule?
A: The Angle-Side-Angle (ASA) rule states that two triangles are congruent if two angles and the side included between them in one triangle are equal to the corresponding two angles and included side of the other triangle.
Q: How do we know that &&\angle BCA = \angle DAC&&?
A: We know this because lines &&l&& and &&m&& are given as parallel, and the diagonal &&AC&& acts as a transversal. The angles &&\angle BCA&& and &&\angle DAC&& are a pair of alternate interior angles, which are always equal when lines are parallel.
Q: What is a transversal line?
A: A transversal is a line that passes through two or more other lines in the same plane at distinct points. In this problem, &&AC&& is a transversal for both pairs of parallel lines.
Q: Why was the ASA rule the best choice here?
A: The ASA rule was the most direct method because the parallel lines allowed us to find two pairs of equal angles (&&\angle BCA = \angle DAC&& and &&\angle BAC = \angle DCA&&). The side included between these angles, &&AC&&, is common to both triangles, which perfectly fits the ASA criteria.
Q: What kind of quadrilateral is &&ABCD&&?
A: The quadrilateral &&ABCD&& is a parallelogram. This is because both pairs of its opposite sides are parallel (line &&l \parallel m&&, and line &&p \parallel q&&).
Further Reading
To revise the concepts of parallel lines, transversals, and congruence rules, you can consult the official NCERT Class 9 textbook on their website: https://ncert.nic.in/.


