NCERT Solutions for Class 9 Maths Exercise 7.1 Question 5

Understanding the Question 🧐
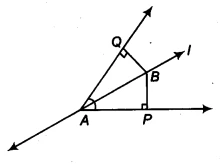
This question explores a fundamental property related to angle bisectors. We are given an angle &&\angle A&& which is bisected by a line &&l&&. From a point &&B&& on this bisector, perpendiculars are drawn to the “arms” of the angle. We need to prove two things: first, that the two right-angled triangles formed are congruent, and second, as a result, that the point &&B&& is at an equal distance from both arms of the angle. These ncert solutions will demonstrate the proof clearly.
Line &&l&& is the bisector of an angle &&\angle A&& and &&B&& is any point on &&l&&. &&BP&& and &&BQ&& are perpendiculars from &&B&& to the arms of &&\angle A&&. Show that:
(i) &&\triangle APB \cong \triangle AQB&&
(ii) &&BP = BQ&& or &&B&& is equidistant from the arms of &&\angle A&&.
Step-by-Step Solution 📝
Part (i): Prove that &&\triangle APB \cong \triangle AQB&&
Step 1: Identify the Given Information
Let’s list what the question tells us, which we will use in our proof:
- Line &&l&& is the bisector of &&\angle A&&. This means it divides &&\angle A&& into two equal angles. So, &&\angle PAB = \angle QAB&&.
- &&BP&& is perpendicular to the arm &&AP&&. This means &&\angle APB = 90^\circ&&.
- &&BQ&& is perpendicular to the arm &&AQ&&. This means &&\angle AQB = 90^\circ&&.
Step 2: Compare the Two Triangles (&&\triangle APB&& and &&\triangle AQB&&)
Now, let’s find the equal parts in both triangles to establish congruence:
- Angle: &&\angle PAB = \angle QAB&& (Given that &&l&& is the angle bisector)
- Angle: &&\angle APB = \angle AQB&& (Both are &&90^\circ&&, as they are perpendiculars)
- Side: &&AB = AB&& (This side is common to both triangles)
Step 3: Apply the Correct Congruence Rule
We have two pairs of equal angles and one pair of equal non-included sides. This set of conditions matches the Angle-Angle-Side (AAS) congruence criterion.
Therefore, by the AAS congruence rule:
&&\triangle APB \cong \triangle AQB&&
Part (ii): Prove that &&BP = BQ&&
This second part is a direct result of the first part.
Since we have already proven in Part (i) that &&\triangle APB \cong \triangle AQB&&, we can use the CPCTC theorem.
CPCTC stands for Corresponding Parts of Congruent Triangles are Congruent (i.e., equal).
In our congruent triangles, the side &&BP&& in &&\triangle APB&& corresponds to the side &&BQ&& in &&\triangle AQB&&.
Therefore, by CPCTC:
&&BP = BQ&&
This equality proves that the point &&B&& is equidistant from the arms of &&\angle A&&.
Conclusion and Key Points ✅
We have successfully demonstrated both parts of the question. First, we proved &&\triangle APB \cong \triangle AQB&& using the AAS congruence rule. Then, using CPCTC, we concluded that &&BP = BQ&&. This exercise proves an important theorem in geometry: any point lying on the bisector of an angle is equidistant from the arms of the angle.
- The AAS congruence rule is used when you have two pairs of equal angles and a pair of non-included sides.
- An angle bisector divides an angle into two equal angles.
- The distance from a point to a line is always measured along the perpendicular from the point to the line.
FAQ (Frequently Asked Questions)
Q: What is the main property proven in this question?
A: This question proves a key geometric theorem: any point on the bisector of an angle is equidistant from the two arms of that angle.
Q: What is the AAS congruence rule?
A: The Angle-Angle-Side (AAS) rule states that two triangles are congruent if two pairs of corresponding angles and a pair of corresponding non-included sides are equal.
Q: How does proving &&\triangle APB \cong \triangle AQB&& help show &&BP = BQ&&?
A: Once the triangles are proven congruent, we can apply the CPCTC (Corresponding Parts of Congruent Triangles are Congruent) theorem. Since &&BP&& and &&BQ&& are corresponding sides of the two congruent triangles, they must be equal in length.
Q: What does it mean for a point to be ‘equidistant’ from two lines?
A: Equidistant means ‘of equal distance’. In geometry, the distance from a point to a line is the length of the perpendicular segment from the point to the line. So, point &&B&& being equidistant from the arms of the angle means the lengths of the perpendiculars &&BP&& and &&BQ&& are equal.
Q: Why was the AAS rule used instead of RHS?
A: The Right-angle-Hypotenuse-Side (RHS) rule requires a right angle, the hypotenuse, and one other corresponding side to be equal. While we had the right angle (at &&P&& and &&Q&&) and a common hypotenuse (&&AB&&), we did not know if any other sides (&&AP&& and &&AQ&&, or &&BP&& and &&BQ&&) were equal at the start. Instead, we knew two pairs of angles were equal (the right angles and the bisected angles) and a non-included side (&&AB&&), which perfectly fits the AAS criterion.
Further Reading
To learn more about the properties of triangles and congruence rules, you can refer to the official NCERT Class 9 textbook on their website: https://ncert.nic.in/.


