NCERT Solutions for Class 9 Maths Exercise 7.1 Question 6

Understanding the Question 🧐
This problem gives us a figure with specific conditions about equal sides and angles. Our task is to use these conditions to prove that two other line segments, &&BC&& and &&DE&&, are equal in length. This is a classic geometry problem that involves proving triangle congruence. Let’s look at the exact question from the ncert solutions textbook.
In the given figure, &&AC = AE&&, &&AB = AD&& and &&∠BAD = ∠EAC&&. Show that &&BC = DE&&.
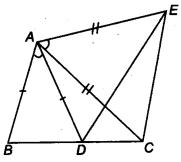
Step-by-Step Solution 📝
To solve this, we will follow a logical sequence of steps. Our main goal is to find two triangles that we can prove are congruent, where &&BC&& and &&DE&& are corresponding sides.
Step 1: List the Given Information
First, let’s clearly write down what we are given in the problem. This helps us see all the tools we have to work with.
- &&AC = AE&&
- &&AB = AD&&
- &&∠BAD = ∠EAC&&
Step 2: Identify the Triangles to Prove Congruent
We need to prove that &&BC = DE&&. Let’s look at the figure and identify which triangles contain these sides.
- The side &&BC&& is part of triangle &&ΔABC&&.
- The side &&DE&& is part of triangle &&ΔADE&&.
Step 3: Manipulate the Angles to Use SAS Rule
To prove &&ΔABC ≅ ΔADE&&, we need to satisfy one of the congruence criteria (like SSS, SAS, ASA). We already have two pairs of equal sides: &&AB = AD&& and &&AC = AE&&. This points towards using the SAS (Side-Angle-Side) rule. For SAS, we need the angle *between* these sides to be equal.
- For &&ΔABC&&, the angle between sides &&AB&& and &&AC&& is &&∠BAC&&.
- For &&ΔADE&&, the angle between sides &&AD&& and &&AE&& is &&∠DAE&&.
We are given &&∠BAD = ∠EAC&&. Notice that &&∠DAC&& is a common part that can be added to both of these angles to get the angles we need.
Let’s add &&∠DAC&& to both sides of the given equation:
&&∠BAD + ∠DAC = ∠EAC + ∠DAC&&
By looking at the figure, we can see that:
- &&∠BAD + ∠DAC = ∠BAC&&
- &&∠EAC + ∠DAC = ∠DAE&&
&&∠BAC = ∠DAE&&
Step 4: Prove Congruence using SAS Rule
Now we have all the components needed to prove the triangles are congruent using the SAS rule.
In &&ΔABC&& and &&ΔADE&&:
- &&AB = AD&& (Given)
- &&∠BAC = ∠DAE&& (Proved in Step 3)
- &&AC = AE&& (Given)
&&ΔABC ≅ ΔADE&&
Step 5: Final Conclusion using CPCTC
Since we have successfully proven that the two triangles are congruent, their corresponding parts must be equal.
The side corresponding to &&BC&& in &&ΔABC&& is the side &&DE&& in &&ΔADE&&.
Therefore,
&&BC = DE&& (By CPCTC)
Hence, we have proved what was required.
Conclusion and Key Points ✅
In this solution, we demonstrated that &&BC = DE&&. The key to the proof was identifying the correct pair of triangles (&&ΔABC&& and &&ΔADE&&) and then manipulating the given angle equality (&&∠BAD = ∠EAC&&) by adding a common angle (&&∠DAC&&) to both sides. This allowed us to establish the equality of the included angles (&&∠BAC = ∠DAE&&), which was necessary to apply the SAS congruence rule. Finally, using CPCTC, we concluded that the corresponding sides &&BC&& and &&DE&& are equal.
- SAS Congruence Rule: Two triangles are congruent if two sides and the *included angle* of one triangle are equal to the two sides and the included angle of the other triangle.
- CPCTC: This stands for “Corresponding Parts of Congruent Triangles are Congruent.” It is a powerful reason you can use *after* you have proven two triangles are congruent.
- Always start by clearly listing the given information and what you need to prove. This helps structure your thoughts.
FAQ
Q: What is the main objective of Question 6 in Exercise 7.1?
A: The main objective is to prove that the length of the line segment &&BC&& is equal to the length of the line segment &&DE&&, using the given conditions in the figure.
Q: Which triangles should be proven congruent to show that &&BC = DE&&?
A: To show that &&BC = DE&&, we need to prove that Triangle &&ABC&& (&&ΔABC&&) is congruent to Triangle &&ADE&& (&&ΔADE&&). &&BC&& and &&DE&& are corresponding sides of these two triangles.
Q: What is the key step in proving the congruence of the triangles in this problem?
A: The key step is to show that &&∠BAC&& is equal to &&∠DAE&&. This is done by adding the common angle &&∠DAC&& to both sides of the given equality, which is &&∠BAD = ∠EAC&&.
Q: Which congruence rule is used to solve this question?
A: The Side-Angle-Side (SAS) congruence rule is used. We use the sides &&AB = AD&&, the included angle &&∠BAC = ∠DAE&&, and the sides &&AC = AE&& to prove that &&ΔABC ≅ ΔADE&&.
Q: What does CPCTC stand for, and how is it applied here?
A: CPCTC stands for ‘Corresponding Parts of Congruent Triangles are Congruent’. After proving that &&ΔABC ≅ ΔADE&&, we can use CPCTC to conclude that their corresponding sides &&BC&& and &&DE&& must be equal.
Q: Why can’t we directly use &&∠BAD&& and &&∠EAC&& for the SAS rule?
A: We cannot use them directly because &&∠BAD&& and &&∠EAC&& are not the *included* angles between the pairs of equal sides in &&ΔABC&& and &&ΔADE&&. For the SAS rule, the angle must be between the two sides, which are &&∠BAC&& and &&∠DAE&& respectively.
Further Reading
For more information on triangles and their properties, you can refer to the official NCERT Class 9 Maths textbook. Visit the official NCERT website for more resources: https://ncert.nic.in/.


