NCERT Solutions for Class 9 Maths Exercise 7.2 Question 6

Welcome to the step-by-step solution for Question 6 of Exercise 7.2 from the chapter on Triangles. This proof cleverly uses the isosceles triangle theorem twice, followed by the angle sum property of a triangle, to reach the result.
| Given Information | &&\triangle ABC&& is an isosceles triangle with &&AB = AC&&. Side BA is produced to D such that &&AD = AB&&. |
|---|---|
| To Prove | &&\angle BCD&& is a right angle (i.e., &&\angle BCD = 90^\circ&&). |
| Key Concepts Used | Isosceles Triangle Theorem and the Angle Sum Property of a Triangle. |
Question 6: &&\triangle ABC&& is an isosceles triangle in which &&AB = AC&&. Side BA is produced to D such that &&AD = AB&&. Show that &&\angle BCD&& is a right angle.
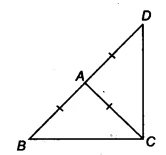
How to Prove &&\angle BCD&& is a Right Angle 🤔
This proof can be completed in five logical steps.
- Step 1: Use the Isosceles Triangle Theorem in &&\triangle ABC&&
Start with the given isosceles triangle ABC. Since it is given that &&AB = AC&&, the angles opposite to these sides must be equal. Therefore, &&\angle ACB = \angle ABC&&. Label this as Equation (1). - Step 2: Show that &&\triangle ACD&& is also an Isosceles Triangle
We are given &&AB = AC&& and &&AD = AB&&. By transitivity (Euclid’s Axiom 1), it follows that &&AD = AC&&. Since two sides of &&\triangle ACD&& are equal, it is also an isosceles triangle. - Step 3: Use the Isosceles Triangle Theorem in &&\triangle ACD&&
Now that we know &&\triangle ACD&& is isosceles, we can state that the angles opposite its equal sides (&&AD&& and &&AC&&) are equal. Therefore, &&\angle ACD = \angle ADC&&. Label this as Equation (2). - Step 4: Apply the Angle Sum Property to the Large Triangle (&&\triangle DBC&&)
Consider the entire triangle DBC. The sum of its three angles is &&180^\circ&&. So, &&\angle DBC + \angle BCD + \angle CDB = 180^\circ&&. Note that &&\angle BCD&& itself is the sum of &&\angle BCA&& and &&\angle ACD&&. - Step 5: Substitute and Solve for &&\angle BCD&&
In the angle sum equation, replace &&\angle DBC&& with &&\angle BCA&& (from Eq 1) and &&\angle CDB&& with &&\angle ACD&& (from Eq 2). The equation becomes &&\angle BCA + (\angle BCA + \angle ACD) + \angle ACD = 180^\circ&&, which simplifies to &&2(\angle BCA + \angle ACD) = 180^\circ&&. Since &&\angle BCA + \angle ACD = \angle BCD&&, we get &&2\angle BCD = 180^\circ&&, which means &&\angle BCD = 90^\circ&&.
Detailed Step-by-Step Proof 📝
Here is the formal proof, written step-by-step.
Given:
In &&\triangle ABC&&, &&AB = AC&&.
Side BA is produced to D such that &&AD = AB&&.
To Prove:
&&\angle BCD = 90^\circ&&.
Proof:
First, in &&\triangle ABC&&, we have:
&&AB = AC&& (Given)
&&\implies \angle ACB = \angle ABC&& (Angles opposite to equal sides are equal) … (Equation 1)
Next, we are given &&AD = AB&&. Since &&AB = AC&&, it implies &&AD = AC&&.
Now, in &&\triangle ACD&&, we have:
&&AD = AC&& (Proved above)
&&\implies \angle ACD = \angle ADC&& (Angles opposite to equal sides are equal) … (Equation 2)
Now, let’s consider the large triangle, &&\triangle DBC&&.
By the angle sum property of a triangle, the sum of all interior angles is &&180^\circ&&.
&&\angle DBC + \angle BDC + \angle BCD = 180^\circ&&
From the figure, we can write the angles as:
&&\angle DBC&& is the same as &&\angle ABC&&.
&&\angle BDC&& is the same as &&\angle ADC&&.
&&\angle BCD = \angle ACB + \angle ACD&&.
Substituting these into the angle sum equation:
&&\angle ABC + \angle ADC + (\angle ACB + \angle ACD) = 180^\circ&&
Now, using Equation 1 and Equation 2, we can replace &&\angle ABC&& with &&\angle ACB&& and &&\angle ADC&& with &&\angle ACD&&:
&&\implies (\angle ACB) + (\angle ACD) + (\angle ACB + \angle ACD) = 180^\circ&&
&&\implies 2\angle ACB + 2\angle ACD = 180^\circ&&
&&\implies 2(\angle ACB + \angle ACD) = 180^\circ&&
Since &&\angle ACB + \angle ACD = \angle BCD&&,
&&\implies 2\angle BCD = 180^\circ&&
&&\implies \angle BCD = \frac{180^\circ}{2} = 90^\circ&&
Conclusion:
&&\angle BCD = 90^\circ&&
Hence, &&\angle BCD&& is a right angle.
Trick: Using Variables to Simplify 💡
The proof can look cleaner with variables.
- In &&\triangle ABC&&, let &&\angle ACB = \angle ABC = x&&.
- In &&\triangle ACD&&, let &&\angle ACD = \angle ADC = y&&.
By the angle sum property:
&&x + y + (x+y) = 180^\circ&&
&&2x + 2y = 180^\circ&&
&&2(x+y) = 180^\circ&&
Since &&\angle BCD = x+y&&, we have &&2\angle BCD = 180^\circ&&, so &&\angle BCD = 90^\circ&&.
FAQ (Frequently Asked Questions)
Q: How do we know that triangle ACD is an isosceles triangle?
A: We are given two facts: &&AB = AC&& and &&AD = AB&&. Since both &&AD&& and &&AC&& are equal to the same segment (&&AB&&), they must be equal to each other (&&AD = AC&&). A triangle with two equal sides is an isosceles triangle.
Q: What is the angle sum property of a triangle?
A: The angle sum property of a triangle states that the sum of the measures of the three interior angles of any triangle is always &&180&& degrees.
Q: Is there a simpler way to write the final substitution step?
A: Yes. You can use variables to simplify. Let &&\angle ACB = x&& and &&\angle ACD = y&&. From the isosceles triangles, we know &&\angle ABC = x&& and &&\angle ADC = y&&. In the large triangle &&\triangle DBC&&, the sum of angles is &&\angle DBC + \angle BCD + \angle BDC = 180^\circ&&. Substituting the variables gives &&x + (x + y) + y = 180^\circ&&. This simplifies to &&2x + 2y = 180^\circ&&, or &&2(x+y) = 180^\circ&&. Since &&\angle BCD = x+y&&, this means &&2\angle BCD = 180^\circ&&, so &&\angle BCD = 90^\circ&&.
Q: Which two main theorems are combined in this proof?
A: This proof effectively combines two fundamental theorems: the Isosceles Triangle Theorem (angles opposite to equal sides are equal) and the Angle Sum Property of a Triangle (all angles sum to &&180^\circ&&).


