NCERT Solutions for Class 9 Maths Exercise 7.3 Question 4

Welcome, students! Let’s solve Question 4 from Exercise 7.3. This question asks us to prove that a triangle is isosceles if its two altitudes are equal, and it specifically requires us to use the RHS congruence rule. This is a great exercise in choosing the right triangles for a proof.
| Given Information | A &&\triangle ABC&& in which altitudes &&BE&& and &&CF&& are equal (&&BE = CF&&). |
|---|---|
| To Prove | &&\triangle ABC&& is an isosceles triangle (i.e., &&AB = AC&&). |
| Required Method | RHS (Right angle-Hypotenuse-Side) congruence rule. |
Question 4: BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
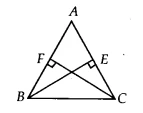
How to Prove &&\triangle ABC&& is Isosceles using RHS Rule 🤔
This proof requires us to carefully select the right triangles to apply the RHS rule.
- Step 1: Identify the Correct Right-Angled Triangles
To use the RHS rule, we need right-angled triangles where we know the hypotenuse. The altitudes &&BE&& and &&CF&& create two right-angled triangles on the common base &&BC&&: &&\triangle BFC&& and &&\triangle CEB&&. These are the correct triangles to compare. - Step 2: List the Known Equal Parts for RHS Congruence
Compare &&\triangle BFC&& and &&\triangle CEB&&. We can identify three equal parts that match the RHS criteria:- Right Angle (R): &&\angle BFC = \angle CEB&& (both are &&90^\circ&& as BE and CF are altitudes).
- Hypotenuse (H): &&BC = CB&& (this side is the hypotenuse for both triangles and is common).
- Side (S): &&CF = BE&& (it is given that the altitudes are equal).
- Step 3: Apply the RHS Congruence Rule
Since the right angle, hypotenuse, and one corresponding side of &&\triangle BFC&& are equal to those of &&\triangle CEB&&, we can conclude that the triangles are congruent by the RHS rule. So, &&\triangle BFC \cong \triangle CEB&&. - Step 4: Use CPCTC to Find Equal Angles
Now that the triangles are congruent, their corresponding parts are equal (CPCTC). This means the corresponding angles &&\angle FBC&& and &&\angle ECB&& are equal. These are the same angles as &&\angle ABC&& and &&\angle ACB&& in the main triangle. - Step 5: Use the Converse of the Isosceles Triangle Theorem
Since we have proved that two angles of &&\triangle ABC&& (&&\angle ABC&& and &&\angle ACB&&) are equal, we can apply the theorem which states that sides opposite to equal angles are equal. Therefore, &&AC = AB&&, which by definition means that &&\triangle ABC&& is an isosceles triangle.
Detailed Step-by-Step Proof 📝
Here is the formal proof, written step-by-step.
Given:
In &&\triangle ABC&&, &&BE&& and &&CF&& are altitudes to sides &&AC&& and &&AB&& respectively.
So, &&\angle BEC = 90^\circ&& and &&\angle BFC = 90^\circ&&.
We are also given that the altitudes are equal: &&BE = CF&&.
To Prove:
&&\triangle ABC&& is an isosceles triangle.
Proof:
To use the RHS rule, we must select two right-angled triangles that share a hypotenuse or have equal hypotenuses. Let’s consider &&\triangle BFC&& and &&\triangle CEB&&.
In &&\triangle BFC&& and &&\triangle CEB&&:
- &&\angle BFC = \angle CEB&& (Each &&90^\circ&&, as CF and BE are altitudes) [R]
- &&BC = CB&& (Common hypotenuse) [H]
- &&CF = BE&& (Given) [S]
Therefore, by the RHS congruence rule, we have:
&&\triangle BFC \cong \triangle CEB&&
Since the two triangles are congruent, their corresponding parts must be equal (by CPCTC).
&&\implies \angle FBC = \angle ECB&& (by CPCTC)
These angles are the same as the base angles of the larger triangle, &&\triangle ABC&&. So, we have:
&&\angle ABC = \angle ACB&&
Now, in &&\triangle ABC&&, we use the converse of the isosceles triangle theorem, which states that if two angles of a triangle are equal, then the sides opposite them are also equal.
Since &&\angle ABC = \angle ACB&&, the sides opposite them must be equal.
&&\implies AC = AB&&
Conclusion:
Since two sides of &&\triangle ABC&& are equal, &&\triangle ABC&& is an isosceles triangle.
Hence, proved.
Choosing the Right Triangles 🖍️
A common mistake is trying to use triangles &&\triangle ABE&& and &&\triangle ACF&&. While that works for an AAS proof, this question *specifically* asks you to use the RHS rule. For RHS, you must identify a right angle, a hypotenuse, and a side. Triangles &&\triangle BFC&& and &&\triangle CEB&& are the correct choice because they share the common hypotenuse &&BC&& and have the other required equal parts.
FAQ (Frequently Asked Questions)
Q: What is the RHS congruence rule?
A: The RHS (Right angle-Hypotenuse-Side) congruence rule is a special criterion for right-angled triangles. It states that if the hypotenuse and one side of a right-angled triangle are equal to the hypotenuse and one corresponding side of another right-angled triangle, then the two triangles are congruent.
Q: Why was it important to choose triangles BFC and CEB for this proof?
A: The question specifically asks to use the RHS rule. This rule requires a right angle, a hypotenuse, and a side. The triangles &&\triangle BFC&& and &&\triangle CEB&& share a common hypotenuse (&&BC&&) and have right angles at F and E. Since we are given that the sides &&CF&& and &&BE&& are equal, these triangles perfectly fit the RHS criteria. Other triangles, like &&\triangle ABE&& and &&\triangle ACF&&, would not work for an RHS proof in this case.
Q: What is the ‘Converse of the Isosceles Triangle Theorem’?
A: It is the opposite of the standard isosceles triangle theorem. It states: ‘If two angles of a triangle are equal, then the sides opposite to those angles are also equal.’ We use this theorem in the final step to prove &&AB = AC&& after showing that &&\angle B = \angle C&&.
Q: How does this proof differ from the one in Exercise 7.2, Question 4?
A: Both questions prove the same result, but they use different methods. In Exercise 7.2, Question 4, the proof is done using the AAS (Angle-Angle-Side) rule with triangles &&\triangle ABE&& and &&\triangle ACF&&. In this question, we are specifically instructed to use the RHS rule, which requires a different pair of triangles (&&\triangle BFC&& and &&\triangle CEB&&).


