NCERT Solutions for Class 9 Maths Exercise 7.3 Question 5

Welcome, students! This guide provides a detailed proof for Question 5 of Exercise 7.3. This problem asks us to formally prove one of the most important theorems about isosceles triangles: that the angles opposite the equal sides are also equal. We will accomplish this by making a simple construction and using the RHS congruence rule.
| Given Information | An isosceles triangle &&\triangle ABC&& with &&AB = AC&&. |
|---|---|
| To Prove | &&\angle B = \angle C&&. |
| Method Used | Construction of an altitude and the RHS congruence rule. |
Question 5: ABC is an isosceles triangle with &&AB = AC&&. Draw &&AP \perp BC&& to show that &&\angle B = \angle C&&.
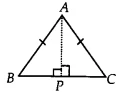
How to Prove &&\angle B = \angle C&& 🤔
This proof can be completed in five logical steps, starting with a key construction.
- Step 1: Perform the Necessary Construction
Start with the given isosceles triangle ABC where &&AB = AC&&. To facilitate the proof, draw a line segment AP from vertex A such that it is perpendicular to the base BC. This line AP is the altitude. - Step 2: Identify the Two Right-Angled Triangles
The construction of the altitude AP divides the main triangle ABC into two right-angled triangles: &&\triangle APB&& and &&\triangle APC&&. The proof will be based on showing that these two triangles are congruent. - Step 3: List the Known Equal Parts for RHS Congruence
Compare &&\triangle APB&& and &&\triangle APC&&. We can identify three equal parts that match the RHS criteria:- Right Angle (R): &&\angle APB = \angle APC&& (both are &&90^\circ&& by construction).
- Hypotenuse (H): &&AB = AC&& (this is given).
- Side (S): &&AP = AP&& (this side is common to both triangles).
- Step 4: Apply the RHS Congruence Rule
Since the right angle, hypotenuse, and one corresponding side of &&\triangle APB&& are equal to those of &&\triangle APC&&, we can conclude that the triangles are congruent by the RHS (Right angle-Hypotenuse-Side) rule. So, &&\triangle APB \cong \triangle APC&&. - Step 5: Use CPCTC to Conclude the Proof
Now that the triangles are proven to be congruent, their corresponding parts must be equal (CPCTC). Therefore, the corresponding angles &&\angle B&& and &&\angle C&& must be equal. Hence, &&\angle B = \angle C&& is proved.
Detailed Step-by-Step Proof 📝
Here is the formal proof, written step-by-step.
Given:
An isosceles triangle &&\triangle ABC&& in which &&AB = AC&&.
To Prove:
&&\angle B = \angle C&&.
Construction:
Draw an altitude AP from vertex A to the side BC. This means that &&AP \perp BC&&, and so &&\angle APB = \angle APC = 90^\circ&&.
Proof:
Now, let’s compare the two right-angled triangles we have formed, &&\triangle APB&& and &&\triangle APC&&.
In &&\triangle APB&& and &&\triangle APC&&:
- &&\angle APB = \angle APC&& (Each &&90^\circ&&, by construction) [R]
- &&AB = AC&& (Given, this is the hypotenuse) [H]
- &&AP = AP&& (Common side) [S]
Therefore, by the RHS congruence rule, we have:
&&\triangle APB \cong \triangle APC&&
Since the two triangles are congruent, all their corresponding parts must be equal (by CPCTC).
The angle corresponding to &&\angle B&& (or &&\angle ABP&&) in &&\triangle APB&& is &&\angle C&& (or &&\angle ACP&&) in &&\triangle APC&&.
Conclusion:
&&\implies \angle B = \angle C&& (by CPCTC)
Hence, it is proved that the angles opposite to the equal sides of an isosceles triangle are equal.
This is a Proof of the Isosceles Triangle Theorem ✅
This question is not just a random problem; it’s a guided proof for a fundamental theorem in geometry. The theorem states: “If two sides of a triangle are equal, then the angles opposite those sides are also equal.” This proof, using the RHS rule, is one of the standard ways to demonstrate why this theorem is true.
FAQ (Frequently Asked Questions)
Q: What is the Isosceles Triangle Theorem?
A: The Isosceles Triangle Theorem states that if two sides of a triangle are equal, then the angles opposite those sides are also equal. This question is a formal proof of this very theorem.
Q: Why is a construction step needed for this proof?
A: A construction (drawing the altitude AP) is needed to create two right-angled triangles. This allows us to use the powerful RHS congruence rule, which is not applicable to the original triangle ABC as it is not necessarily a right-angled triangle.
Q: What is the RHS congruence rule?
A: The RHS (Right angle-Hypotenuse-Side) congruence rule is a special criterion for right-angled triangles. It states that if the hypotenuse and one side of a right-angled triangle are equal to the hypotenuse and one corresponding side of another right-angled triangle, then the two triangles are congruent.
Q: Is the converse of the Isosceles Triangle Theorem also true?
A: Yes, the converse is also a valid theorem. It states that if two angles of a triangle are equal, then the sides opposite to those angles are also equal.


