NCERT Solutions for Class 9 Maths Exercise 8.1 Question 6

Welcome to the solution for Question 6 of Exercise 8.1. This is a two-part proof where we use the properties of a parallelogram, specifically alternate interior angles, to prove that the shape is actually a rhombus.
| Given Information | A parallelogram ABCD where the diagonal AC bisects &&\angle A&&. |
|---|---|
| To Prove | (i) The diagonal AC also bisects &&\angle C&&. (ii) The parallelogram ABCD is a rhombus. |
| Key Concepts Used | Alternate Interior Angles, Converse of Isosceles Triangle Theorem. |
Question 6: Diagonal AC of a parallelogram ABCD bisects &&\angle A&&. Show that (i) it bisects &&\angle C&& also, (ii) ABCD is a rhombus.
Detailed Step-by-Step Proof 📝
We will prove each of the two parts in sequence.
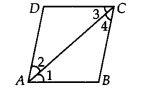
(i) Prove that AC bisects &&\angle C&&
Given: ABCD is a parallelogram, and AC bisects &&\angle A&&.
This means &&\angle DAC = \angle BAC&& … (1)
Since ABCD is a parallelogram, its opposite sides are parallel.
1. Consider &&AB \parallel DC&& with transversal AC:
The alternate interior angles must be equal.
&&\implies \angle BAC = \angle DCA&& … (2)
2. Consider &&AD \parallel BC&& with transversal AC:
The alternate interior angles must be equal.
&&\implies \angle DAC = \angle BCA&& … (3)
Combining the results:
From equations (1), (2), and (3), we can equate all the angles:
&&\angle DAC = \angle BAC = \angle DCA = \angle BCA&&
Now, focusing on the angles at vertex C, we have found that &&\angle DCA = \angle BCA&&.
Therefore, the diagonal AC also bisects &&\angle C&&.
(ii) Prove that ABCD is a rhombus
To prove that the parallelogram is a rhombus, we need to show that a pair of its adjacent sides are equal.
From the proof in part (i), we established that all four angles created by the diagonal are equal. Let’s focus on &&\triangle ABC&& and the angles within it.
We know that &&\angle BAC = \angle BCA&&.
Now, we use the Converse of the Isosceles Triangle Theorem, which states that if two angles in a triangle are equal, the sides opposite to them are also equal.
- The side opposite to &&\angle BCA&& is &&AB&&.
- The side opposite to &&\angle BAC&& is &&BC&&.
Therefore, &&AB = BC&&.
Since ABCD is a parallelogram with a pair of equal adjacent sides, it satisfies the definition of a rhombus.
Therefore, ABCD is a rhombus.
Key Property of a Rhombus ✅
This proof establishes a key property that defines a rhombus: the diagonals of a rhombus bisect the vertex angles. This problem shows that if this property holds true for even one angle in a parallelogram, the shape must be a rhombus.
FAQ (Frequently Asked Questions)
Q: What are the key properties of a parallelogram used in this proof?
A: The most important property used here is that opposite sides are parallel (&&AB \parallel DC&& and &&AD \parallel BC&&). This allows us to use the property that alternate interior angles are equal when a transversal (the diagonal AC) cuts across the parallel lines.
Q: What is the difference between a parallelogram and a rhombus?
A: A parallelogram is a quadrilateral with two pairs of parallel sides. A rhombus is a special type of parallelogram where all four sides are equal in length. This proof shows that if a diagonal of a parallelogram bisects an angle, it forces the adjacent sides to be equal, thus making it a rhombus.
Q: What is the ‘Converse of the Isosceles Triangle Theorem’?
A: The ‘Converse of the Isosceles Triangle Theorem’ states that if two angles of a triangle are equal, then the sides opposite to those angles are also equal. We use this in the proof to show that &&AB = BC&& after establishing that &&\angle BAC = \angle BCA&&.
Q: Does this property apply to both diagonals of the rhombus?
A: Yes. This proof shows that if one diagonal bisects a vertex angle in a parallelogram, it must be a rhombus. A key property of all rhombuses is that both of their diagonals bisect the vertex angles.


