NCERT Solutions for Class 9 Maths Exercise 6.2 Question 2

Understanding the Question 🧐
In this problem, we are given a figure with three parallel lines intersected by a transversal line. We are told that line &&AB&& is parallel to line &&CD&&, and line &&CD&& is parallel to line &&EF&&. We are also given a ratio between two angles, &&y&& and &&z&&, as &&y : z = 3 : 7&&. Our goal is to find the value of angle &&x&&. This question tests our understanding of the properties of parallel lines, specifically alternate interior angles and consecutive interior angles. Let’s find the ncert solutions step-by-step.
In Fig. 6.29, if &&AB \parallel CD&&, &&CD \parallel EF&& and &&y : z = 3 : 7&&, find &&x&&.
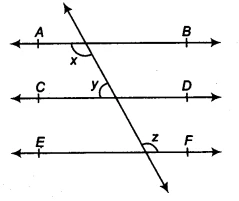
Step-by-Step Solution 📝
Here’s a detailed breakdown of how to solve this problem.
Step 1: Identify the given information.
- Line &&AB \parallel CD&&.
- Line &&CD \parallel EF&&.
- The ratio of angles &&y&& and &&z&& is &&y : z = 3 : 7&&.
Step 2: Use the properties of parallel lines to relate the angles.
A key theorem states that lines parallel to the same line are parallel to each other. Since &&AB \parallel CD&& and &&CD \parallel EF&&, it follows that &&AB \parallel EF&&.
Now that we know &&AB \parallel EF&&, we can relate angles &&x&& and &&z&&. Notice that &&x&& and &&z&& are alternate interior angles. For parallel lines, alternate interior angles are equal.
&&x = z&& … (Equation 1)
Next, let’s consider the relationship between &&x&& and &&y&&. Since we are given that &&AB \parallel CD&&, the angles &&x&& and &&y&& are consecutive interior angles (or co-interior angles). The sum of consecutive interior angles is always &&180^\circ&&.
&&x + y = 180^\circ&& … (Equation 2)
Step 3: Use the ratio to find the values of the angles.
We can combine our findings. From Equation 1, we know &&x = z&&. Let’s substitute this into Equation 2:
&&z + y = 180^\circ&&
We are given the ratio &&y : z = 3 : 7&&. Let’s introduce a common ratio multiplier, say ‘&&a&&’. This means:
- &&y = 3a&&
- &&z = 7a&&
Now, substitute these into our equation &&z + y = 180^\circ&&:
&&7a + 3a = 180^\circ&&
&&10a = 180^\circ&&
&&a = \frac{180^\circ}{10}&&
&&a = 18^\circ&&
Step 4: Calculate the final value of x.
Now that we have the value of &&a&&, we can find &&z&&.
&&z = 7a = 7 \times 18^\circ = 126^\circ&&
From Equation 1, we established that &&x = z&&. Therefore:
&&x = 126^\circ&&
Conclusion and Key Points ✅
By using the properties of parallel lines and the given ratio, we successfully determined the value of &&x&&. The final answer is &&x = 126^\circ&&. The key steps involved recognizing that &&x=z&& (alternate interior angles) and that &&x+y=180^\circ&& (consecutive interior angles), which leads to &&y+z=180^\circ&&. This allowed us to solve for the angles using their ratio.
- Lines parallel to the same line: If line ‘a’ is parallel to line ‘b’ and line ‘b’ is parallel to line ‘c’, then line ‘a’ is parallel to line ‘c’. In our case, &&AB \parallel EF&&.
- Alternate Interior Angles: When a transversal intersects two parallel lines, the alternate interior angles formed are equal. (e.g., &&x = z&&).
- Consecutive Interior Angles: When a transversal intersects two parallel lines, the consecutive interior angles are supplementary, meaning their sum is &&180^\circ&&. (e.g., &&x + y = 180^\circ&&).
FAQ 🙋♂️
Q: What are consecutive interior angles?
A: Consecutive interior angles are a pair of angles that lie on the same side of the transversal and are ‘inside’ or between the two parallel lines. Their sum is always &&180^\circ&&.
Q: Why is &&x = z&& in this problem?
A: Since line &&AB \parallel CD&& and &&CD \parallel EF&&, it means &&AB \parallel EF&&. The angles &&x&& and &&z&& are alternate interior angles with respect to the parallel lines &&AB&& and &&EF&&. A property of parallel lines states that alternate interior angles are equal, hence &&x = z&&.
Q: How do we use the ratio &&y : z = 3 : 7&& to find the angles?
A: A ratio represents a proportional relationship. We assume the angles are &&y = 3a&& and &&z = 7a&& for some constant &&a&&. We then use a geometric property, like &&y + z = 180^\circ&&, to form an equation: &&3a + 7a = 180^\circ&&. Solving this gives &&a = 18^\circ&&, which helps us find the actual angle measures.
Q: What does it mean for angles to be supplementary?
A: Two angles are supplementary if their sum is equal to &&180^\circ&&. For example, consecutive interior angles are always supplementary.
Q: If &&AB \parallel CD&& and &&CD \parallel EF&&, why is &&AB \parallel EF&&?
A: This is a fundamental theorem in Euclidean geometry. It states that two lines that are parallel to a third line are also parallel to each other. It’s a transitive property of parallel lines.
Further Reading 📚
For more information on the properties of lines and angles, you can refer to the official NCERT textbook for Class 9 Maths. The concepts are explained in Chapter 6. You can download the textbook from the official NCERT website at https://ncert.nic.in/.


