NCERT Solutions for Class 9 Maths Exercise 6.2 Question 4

Understanding the Question 🧐
In this problem, we are given two parallel lines and two angles, and we need to find a third angle. At first glance, it might not seem straightforward because the lines forming the angle we need to find (`&&∠QRS&&`) are not simple transversals. This problem requires a small construction to reveal the relationships between the angles. These types of questions are common in exams and are a great way to practice using the properties of parallel lines provided in the ncert solutions.
In the given figure, if &&PQ || ST&&, &&∠PQR = 110^\circ&&, and &&∠RST = 130^\circ&&, find &&∠QRS&&.
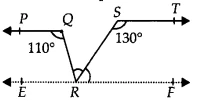
Given Information:
- Line &&PQ&& is parallel to line &&ST&& (i.e., &&PQ || ST&&).
- &&\angle PQR = 110^\circ&&.
- &&\angle RST = 130^\circ&&.
To Find:
- The measure of &&\angle QRS&&.
Solution: Step-by-Step Breakdown 📝
To solve this, we will start by drawing an extra line to help us.
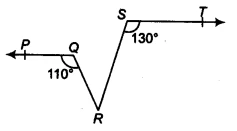
Step 1: Construction 🏗️
The key to solving this problem is to draw a line `XY` through point `R` such that `XY` is parallel to `ST`.
Since we are given that &&PQ || ST&& and we constructed &&XY || ST&&, it follows that all three lines are parallel to each other: &&PQ || XY || ST&&.
Step 2: Find &&\angle QRX&&
Now, consider the parallel lines &&PQ&& and &&XY&& with &&QR&& as the transversal.
The angles &&\angle PQR&& and &&\angle QRX&& are consecutive interior angles (or co-interior angles). A property of parallel lines states that consecutive interior angles are supplementary, meaning their sum is &&180^\circ&&.
So, &&\angle PQR + \angle QRX = 180^\circ&&
Substitute the given value of &&\angle PQR&&:
&&110^\circ + \angle QRX = 180^\circ&&
&&\angle QRX = 180^\circ – 110^\circ&&
&&\angle QRX = 70^\circ&&
Step 3: Find &&\angle SRY&&
Next, consider the parallel lines &&ST&& and &&XY&& with &&SR&& as the transversal.
Similarly, the angles &&\angle RST&& and &&\angle SRY&& are consecutive interior angles.
Therefore, their sum is also &&180^\circ&&.
&&\angle RST + \angle SRY = 180^\circ&&
Substitute the given value of &&\angle RST&&:
&&130^\circ + \angle SRY = 180^\circ&&
&&\angle SRY = 180^\circ – 130^\circ&&
&&\angle SRY = 50^\circ&&
Step 4: Calculate &&\angle QRS&&
We know that &&XY&& is a straight line, so the angle on the line at point &&R&& is &&180^\circ&&. From our construction and the figure, we can see that the straight angle &&\angle XRY&& is made up of three adjacent angles: &&\angle QRX&&, &&\angle QRS&&, and &&\angle SRY&&.
Therefore, &&\angle QRX + \angle QRS + \angle SRY = 180^\circ&&
Now, substitute the values we found in the previous steps:
&&70^\circ + \angle QRS + 50^\circ = 180^\circ&&
&&120^\circ + \angle QRS = 180^\circ&&
To find &&\angle QRS&&, subtract &&120^\circ&& from &&180^\circ&&:
&&\angle QRS = 180^\circ – 120^\circ&&
&&\angle QRS = 60^\circ&&
Conclusion and Key Points ✅
By using a simple construction and applying the property of consecutive interior angles, we found the required angle.
The final answer is: &&\angle QRS = 60^\circ&&.
- A straight line has an angle of &&180^\circ&&.
- When a transversal intersects two parallel lines, the sum of consecutive interior angles is &&180^\circ&&.
- Sometimes, a simple construction is necessary to solve a geometry problem.
Frequently Asked Questions (FAQ)
Q: What is the key first step to solve this problem?
A: The key first step is a construction. You need to draw a new line that passes through point &&R&& and is parallel to the given parallel lines &&PQ&& and &&ST&&. This construction creates new angles that are easier to work with.
Q: What are consecutive interior angles?
A: Consecutive interior angles (or co-interior angles) are a pair of angles on the same side of a transversal and between the two parallel lines. A key property is that they are supplementary, meaning their sum is always &&180^\circ&&.
Q: How is the property of consecutive interior angles used in this solution?
A: This property is used twice. First, to find the angle adjacent to &&\angle PQR = 110^\circ&&. Second, to find the angle adjacent to &&\angle RST = 130^\circ&&. Both calculations rely on the fact that the sum of each pair of consecutive interior angles is &&180^\circ&&.
Q: Why do the angles around point R on the constructed line help find the answer?
A: The constructed line is a straight line, so the angle of the line itself is &&180^\circ&&. This straight angle is composed of three adjacent angles, two of which we calculate (&&\angle QRX = 70^\circ&& and &&\angle SRY = 50^\circ&&) and the third being the unknown angle &&\angle QRS&&. By setting their sum equal to &&180^\circ&&, we can solve for &&\angle QRS&&.
Q: Can this problem be solved without any construction?
A: While there might be other complex methods, the simplest and most standard way to solve this problem involves the construction of a parallel line. The construction directly applies the theorems of parallel lines and transversals to find the solution.
Q: What is the final value of angle QRS?
A: By following the steps of construction and applying angle properties, the final value of angle &&\angle QRS&& is calculated to be &&60^\circ&&.
Further Reading
For more details on the properties of lines and angles, you can refer to the official NCERT textbook provided by the National Council of Educational Research and Training. Visit their website at https://ncert.nic.in/ for official resources.


