NCERT Solutions for Class 9 Maths Exercise 7.1 Question 3

Understanding the Question 🧐
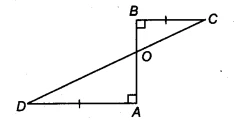
In this problem, we’re given a line segment &&AB&&, with two other line segments, &&AD&& and &&BC&&, drawn perpendicular to it. We’re told these two perpendiculars are equal in length. Our task is to show that the line &&CD&&, which connects the ends of the perpendiculars, cuts &&AB&& into two equal halves. This is known as proving that &&CD&& bisects &&AB&&. The core strategy will be to prove two triangles are congruent. These ncert solutions will show you how.
&&AD&& and &&BC&& are equal perpendiculars to a line segment &&AB&&. Show that &&CD&& bisects &&AB&&.
Step-by-Step Solution 📝
Let’s assume the line segments &&CD&& and &&AB&& intersect at a point &&O&&. Our goal is to prove that &&OA = OB&&.
Step 1: Identify the Given Information
From the question, we can list the facts:
- &&BC \perp AB&&, which means &&\angle OBC = 90^\circ&&.
- &&AD \perp AB&&, which means &&\angle OAD = 90^\circ&&.
- The perpendiculars are equal: &&AD = BC&&.
Step 2: Choose the Triangles to Compare
The intersecting lines form two triangles: &&\triangle OBC&& and &&\triangle OAD&&. To prove &&OA = OB&&, we can try to prove these two triangles are congruent.
Step 3: Find Equal Parts in Both Triangles
Let’s compare &&\triangle OBC&& and &&\triangle OAD&&:
- Angle: &&\angle OBC = \angle OAD&& (Both are &&90^\circ&&, as given)
- Angle: &&\angle BOC = \angle AOD&& (These are vertically opposite angles, which are always equal)
- Side: &&BC = AD&& (This is given in the question)
Step 4: Apply the Correct Congruence Rule
We have found two equal angles and one equal non-included side. This combination fits the Angle-Angle-Side (AAS) congruence criterion.
So, by the AAS congruence rule, we can state that:
&&\triangle OBC \cong \triangle OAD&&
Step 5: Use CPCTC to Reach the Conclusion
Now that we have proven the triangles are congruent, we can use CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
The side &&OB&& in &&\triangle OBC&& corresponds to the side &&OA&& in &&\triangle OAD&&.
Therefore, by CPCTC, we can conclude that &&OB = OA&&.
Since &&O&& is a point on &&AB&& such that &&OA = OB&&, it means &&O&& is the midpoint of &&AB&&. This proves that &&CD&& bisects &&AB&&.
Conclusion and Key Points ✅
We successfully proved that &&CD&& bisects &&AB&&. The solution involved identifying two triangles (&&\triangle OBC&& and &&\triangle OAD&&), proving them congruent using the AAS congruence rule, and finally using CPCTC to show that &&OA = OB&&.
- AAS Congruence Rule: Two triangles are congruent if any two pairs of angles and one pair of corresponding non-included sides are equal.
- Vertically Opposite Angles: When two lines intersect, the angles opposite each other at the vertex are equal.
- Bisect: To cut something into two equal parts.
FAQ (Frequently Asked Questions)
Q: What does it mean for ‘CD to bisect AB’?
A: It means that the line segment &&CD&& cuts the line segment &&AB&& into two parts of equal length. If they intersect at a point &&O&&, it means that &&OA = OB&&.
Q: What congruence rule was used in this proof?
A: The Angle-Angle-Side (AAS) congruence rule was used to prove that &&\triangle OAD \cong \triangle OBC&&.
Q: Why is &&\angle AOD&& equal to &&\angle BOC&&?
A: These angles are vertically opposite angles. Vertically opposite angles are formed when two straight lines intersect (in this case, &&AB&& and &&CD&&), and they are always equal to each other.
Q: Why was the AAS rule used instead of the ASA rule?
A: For the Angle-Side-Angle (ASA) rule, the equal side must be located between the two equal angles. In this problem, the equal side (&&AD = BC&&) is not between the pairs of equal angles (&& \angle OAD, \angle AOD && and && \angle OBC, \angle BOC &&), so we must use the AAS rule.
Q: How did proving the triangles congruent solve the problem?
A: Once we proved &&\triangle OAD \cong \triangle OBC&&, we could use CPCTC (Corresponding Parts of Congruent Triangles are Congruent). This allowed us to state that their corresponding sides are equal, which gave us &&OA = OB&&. This is the precise condition needed to show that &&CD&& bisects &&AB&&.
Further Reading
For more examples and a deeper dive into the criteria for congruence of triangles, refer to your official NCERT Class 9 textbook. You can also visit the NCERT website at https://ncert.nic.in/.


