NCERT Solutions for Class 9 Maths Exercise 7.3 Question 3

Welcome, students! Let’s break down the solution for Question 3 of Exercise 7.3. This is a great two-part proof that shows how to use the properties of a median to prove the congruence of both smaller and larger triangles.
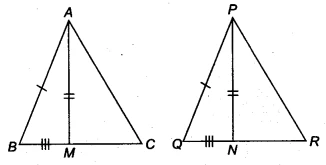
| Given Information | In &&\triangle ABC&& and &&\triangle PQR&&, we have &&AB = PQ&&, &&BC = QR&&, and median &&AM =&& median &&PN&&. |
|---|---|
| To Prove | (i) &&\triangle ABM \cong \triangle PQN&& (ii) &&\triangle ABC \cong \triangle PQR&& |
| Key Concepts Used | Properties of a median, SSS congruence rule, and SAS congruence rule. |
Question 3: Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of &&\triangle PQR&&. Show that: (i) &&\triangle ABM \cong \triangle PQN&& and (ii) &&\triangle ABC \cong \triangle PQR&&
Detailed Step-by-Step Proof 📝
We will prove each part sequentially, as the first result is needed to prove the second.
(i) Prove that &&\triangle ABM \cong \triangle PQN&&
Given:
In &&\triangle ABC&& and &&\triangle PQR&&,
- &&AB = PQ&&
- &&BC = QR&&
- Median &&AM =&& Median &&PN&&
Since AM is the median of &&\triangle ABC&&, it bisects the side BC.
&&\implies BM = \frac{1}{2} BC&&
Similarly, since PN is the median of &&\triangle PQR&&, it bisects the side QR.
&&\implies QN = \frac{1}{2} QR&&
As we are given &&BC = QR&&, their halves must also be equal.
&&\implies \frac{1}{2} BC = \frac{1}{2} QR&&
&&\implies BM = QN&&
Now, let’s compare &&\triangle ABM&& and &&\triangle PQN&&:
- &&AB = PQ&& (Given) [S]
- &&BM = QN&& (Proved above) [S]
- &&AM = PN&& (Given) [S]
Therefore, by the SSS (Side-Side-Side) congruence rule:
&&\triangle ABM \cong \triangle PQN&&
(ii) Prove that &&\triangle ABC \cong \triangle PQR&&
From part (i), we proved that &&\triangle ABM \cong \triangle PQN&&.
Using CPCTC (Corresponding Parts of Congruent Triangles are equal), we can state that their corresponding angles are equal.
&&\implies \angle ABM = \angle PQN&& (by CPCTC)
This is the same as &&\angle ABC = \angle PQR&&, or simply &&\angle B = \angle Q&&.
Now, let’s compare the larger triangles &&\triangle ABC&& and &&\triangle PQR&&:
- &&AB = PQ&& (Given) [S]
- &&\angle ABC = \angle PQR&& (Proved above) [A]
- &&BC = QR&& (Given) [S]
Therefore, by the SAS (Side-Angle-Side) congruence rule:
&&\triangle ABC \cong \triangle PQR&&
The Role of the Median ✅
This problem highlights the importance of understanding what a median is. The key to the first part of the proof was realizing that since &&BC = QR&&, their halves (created by the medians) must also be equal. This provided the third side needed for the SSS congruence rule.
FAQ (Frequently Asked Questions)
Q: What is a median of a triangle?
A: A median of a triangle is a line segment that joins a vertex to the midpoint of the opposite side. A key property is that it divides the opposite side into two equal halves. For example, since AM is the median to BC, it means &&BM = MC&&.
Q: Why is it necessary to prove the smaller triangles (&&\triangle ABM&& and &&\triangle PQN&&) congruent first?
A: To prove the larger triangles (&&\triangle ABC&& and &&\triangle PQR&&) congruent, we are initially given two equal sides (&&AB=PQ&& and &&BC=QR&&). To use the SAS rule, we need the angle between these sides (&&\angle B&& and &&\angle Q&&) to be equal. We don’t know this at the start. Proving the smaller triangles congruent first allows us to use CPCTC to establish that &&\angle B = \angle Q&&, providing the missing piece of information.
Q: What is the SSS congruence rule?
A: The SSS (Side-Side-Side) congruence rule states that if three sides of one triangle are equal to the three corresponding sides of another triangle, then the two triangles are congruent.
Q: What is the SAS congruence rule?
A: The SAS (Side-Angle-Side) congruence rule states that if two sides and the included angle (the angle between those two sides) of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.


