NCERT Solutions for Class 9 Maths Exercise 3.1 Question 1

Understanding the Question 🧐
This question introduces us to the core idea of coordinate geometry using a real-world example. It asks how we can describe the exact position of an object (a table lamp) on a flat surface (a study table). To do this, we need a system of references. This question helps us build the foundation for plotting points on a graph. These ncert solutions will guide you through the logical steps to define any position accurately.
blob:https://ncertsolutions.it.com/019b1816-c674-4c8a-aa28-f540444451b2How will you describe the position of a table lamp on your study table to another person?
Step-by-Step Solution 📝
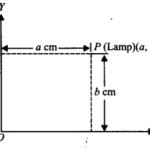
To describe the position of the lamp to someone else, you need a clear and consistent method so they can find the exact same spot. We can achieve this by treating the table as a mathematical plane and assigning coordinates to the lamp’s position.
Here’s how you can do it:
-
Consider the Table as a Plane: The flat top of your study table can be thought of as a Cartesian plane. This is a 2-dimensional surface where we can locate any point.
-
Choose Reference Lines (Axes): To locate a point on a plane, we need two reference lines. Let’s choose two adjacent edges of the rectangular table. Let’s call the longer edge the &&x&&-axis and the shorter edge the &&y&&-axis.
-
Identify the Origin: The corner where these two edges meet is our starting point, called the origin. The coordinates of the origin are &&(0, 0)&&.
-
Measure the Perpendicular Distances: Now, measure the distance of the table lamp from both edges you chose.
- Measure the perpendicular distance of the lamp from the shorter edge (the &&y&&-axis). Let’s say this distance is 20 cm. This will be our &&x&&-coordinate.
- Measure the perpendicular distance of the lamp from the longer edge (the &&x&&-axis). Let’s say this distance is 30 cm. This will be our &&y&&-coordinate.
-
State the Position as Coordinates: The position of the lamp can now be described by these two measurements, written as an ordered pair &&(x, y)&&. Using our measurements, the position of the lamp is &&(20, 30)&&.
So, you can tell the other person: “Considering the corner on the left as the origin, the longer edge as the &&x&&-axis and the shorter edge as the &&y&&-axis, the lamp is located at the point &&(20, 30)&&.” This gives them a precise location that they can find without any confusion.
Conclusion and Key Points ✅
To uniquely describe the position of any object on a flat surface, we can establish a coordinate system. This involves choosing two perpendicular reference lines (axes) and measuring the perpendicular distances of the object from these lines. The position is then represented by an ordered pair of these distances, known as coordinates, in the form &&(x, y)&&.
- Any flat surface can be treated as a 2D Cartesian plane.
- Two perpendicular reference lines are needed, called the axes.
- The point where the axes intersect is the origin, denoted as &&(0, 0)&&.
- The position of a point is written as an ordered pair &&(x, y)&&.
- The order matters! The position &&(20, 30)&& is different from the position &&(30, 20)&&.
FAQ
Q: What is a Cartesian plane in the context of a study table?
A: A Cartesian plane is a flat surface, like your tabletop, defined by two perpendicular lines. We can choose two adjacent edges of the table to act as these lines, called the &&x&&-axis and the &&y&&-axis.
Q: Why do we need two edges (axes) to describe the lamp’s position?
A: Using only one edge tells you the distance along one line, but the lamp could be anywhere along that line. A second, perpendicular edge is needed to pinpoint a unique, exact location on the table surface.
Q: What does an ordered pair like &&(20, 30)&& represent for the table lamp?
A: The ordered pair &&(20, 30)&& represents the coordinates. The first number (the &&x&&-coordinate, &&20&&) is the perpendicular distance from the vertical edge (the &&y&&-axis), and the second number (the &&y&&-coordinate, &&30&&) is the perpendicular distance from the horizontal edge (the &&x&&-axis).
Q: Is the position &&(20, 30)&& the same as &&(30, 20)&&?
A: No, they are different positions. The order in coordinates is crucial. &&(20, 30)&& means a distance of &&20&& units from the vertical edge and &&30&& from the horizontal one, while &&(30, 20)&& means the opposite.
Q: What is the ‘origin’ on the study table?
A: The origin, denoted as &&(0, 0)&&, is the corner of the table where the two edges you chose as your axes meet.
Further Reading
For more concepts on Coordinate Geometry, you can refer to the official NCERT textbook on the NCERT website.